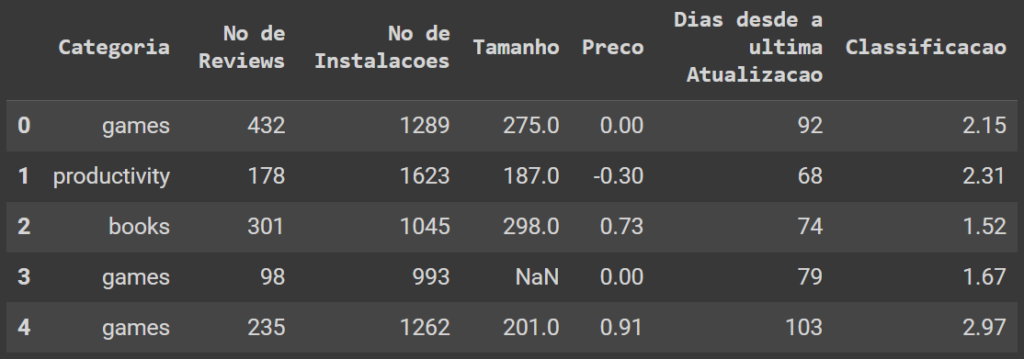
Projeto Prático de Regressão com Python e Scikit-Learn

A ideia do projeto é construir um modelo de regressão para um dataset armazenado em um arquivo chamado reviews.csv. O arquivo é estruturado com 7 colunas. O objetivo final do projeto é fazer um modelo de regressão para fazer previsões da classificação de um aplicativo. O projeto terá várias tarefas e a cada tarefas teremos algumas atividades a serem executadas.

Tarefa 1: Importar as libraries e carregar os dados.

Neste projeto, você irá trabalhar com um conjunto de dados de reviews de aplicativos. Siga as instruções abaixo para concluir as atividades:

Importe as bibliotecas necessárias:
- Importe a biblioteca NumPy com o alias ‘np'.
- Importe a biblioteca pandas com o alias ‘pd'.
- Importe as bibliotecas matplotlib e matplotlib.pyplot com o alias ‘plt'.
Especifique o backend para Matplotlib:
- Adicione a linha ‘%matplotlib inline' para permitir que os gráficos sejam exibidos diretamente no notebook.
Carregue os dados:
- Utilize a função ‘pd.read_csv()' para carregar o arquivo ‘reviews.csv' em um DataFrame chamado ‘df'.
- Certifique-se de que o arquivo ‘reviews.csv' esteja no mesmo diretório do notebook ou especifique o caminho completo para o arquivo.
Explore os dados:
- Use a função ‘df.head()' para exibir as primeiras linhas do DataFrame e ter uma visão geral dos dados carregados.

Tarefa 2: Explorar os Dados

Verificar valores faltando:
- Utilize a função ‘df.isnull().sum()' para verificar se existem valores faltando em cada coluna do DataFrame.
- Analise a saída para identificar quais colunas possuem valores faltando e a quantidade de valores faltando em cada uma delas.
Plotar histogramas das colunas numéricas:
- Selecione as colunas numéricas do DataFrame utilizando ‘df.select_dtypes(include=[np.number])'.
- Utilize o método ‘hist()' para plotar um histograma de cada coluna numérica.
- Customize o tamanho da figura e o número de subplots usando os parâmetros ‘figsize' e ‘layout' para melhor visualização.
- Adicione títulos aos subplots e ao histograma geral usando ‘plt.suptitle()' e ‘plt.title()'.
- Ajuste o espaçamento entre os subplots com ‘plt.tight_layout()' para evitar sobreposição.
Gerar estatísticas descritivas:
- Utilize a função ‘df.describe()' para gerar estatísticas descritivas sobre as colunas numéricas do DataFrame.
- Analise a saída para obter informações como média, desvio padrão, mínimo, máximo e quartis de cada coluna numérica.

Tarefa 3: Check de Valores Inválidos

Nesta tarefa, você irá verificar se existem valores inválidos ou inconsistentes nos dados. Siga as instruções abaixo:

Verificar a coluna “Classificacao”:
- Verifique se a coluna “Classificacao” contém apenas valores numéricos válidos.
- Utilize a função pd.to_numeric() com o parâmetro errors='coerce' para converter a coluna “Classificacao” em tipo numérico. Isso substituirá quaisquer valores não numéricos por NaN (Not a Number).
- Conte a quantidade de valores NaN na coluna “Classificacao” usando a função isnull().sum() para identificar quantos valores inválidos existem.
Verificar a coluna “Preco”:
- Verifique se a coluna “Preco” contém apenas valores numéricos válidos.
- Utilize a função pd.to_numeric() com o parâmetro errors='coerce' para converter a coluna “Preco” em tipo numérico.
- Conte a quantidade de valores NaN na coluna “Preco” usando a função isnull().sum() para identificar quantos valores inválidos existem.
Verificar a coluna “Tamanho”:
- Verifique se a coluna “Tamanho” contém apenas valores numéricos válidos.
- Utilize a função pd.to_numeric() com o parâmetro errors='coerce' para converter a coluna “Tamanho” em tipo numérico.
- Conte a quantidade de valores NaN na coluna “Tamanho” usando a função isnull().sum() para identificar quantos valores inválidos existem.
Verificar a coluna “Dias desde a ultima Atualizacao”:
- Verifique se a coluna “Dias desde a ultima Atualizacao” contém apenas valores numéricos válidos.
- Utilize a função pd.to_numeric() com o parâmetro errors='coerce' para converter a coluna “Dias desde a ultima Atualizacao” em tipo numérico.
- Conte a quantidade de valores NaN na coluna “Dias desde a ultima Atualizacao” usando a função isnull().sum() para identificar quantos valores inválidos existem.

Após realizar essas verificações, você terá uma ideia de quantos valores inválidos existem em cada uma dessas colunas.

Lembre-se de que a presença de valores inválidos pode afetar a qualidade e a confiabilidade das análises posteriores. Portanto, é importante tratar esses valores de forma adequada antes de prosseguir.

Se encontrar valores inválidos, você pode optar por removê-los ou substituí-los por um valor adequado, dependendo do contexto e da abordagem escolhida para lidar com dados ausentes.

Tarefa 4: Remover Linhas Inválidas

Nesta tarefa, você irá remover as linhas inválidas do DataFrame. Siga as instruções abaixo:

Remover linhas com valores ausentes:
- Utilize a função dropna() para remover todas as linhas que contêm valores ausentes (NaN) em qualquer coluna.
- Especifique o parâmetro inplace=True para modificar o DataFrame original df diretamente, sem criar uma nova cópia.
Selecionar linhas com valores não-negativos:
- Crie uma máscara booleana usando a condição (df['Dias desde a ultima Atualizacao'] >= 0) & (df['Classificacao'] >= 0).
- Essa máscara deve selecionar as linhas onde os valores das colunas “Dias desde a ultima Atualizacao” e “Classificacao” são maiores ou iguais a zero.
- Atualize o DataFrame df para conter apenas as linhas selecionadas pela máscara.
Verificar o número de linhas restantes:
- Utilize o atributo shape para obter as dimensões do DataFrame df após a remoção das linhas inválidas.
- Imprima o número de linhas restantes usando df.shape[0], que retorna o número de linhas (primeiro elemento da tupla retornada por shape).

Após executar essas etapas, o DataFrame df terá apenas as linhas válidas, onde as colunas “Dias desde a ultima Atualizacao” e “Classificacao” possuem valores não-negativos. O número de linhas restantes será impresso, indicando quantas linhas permaneceram após a remoção das linhas inválidas.

Certifique-se de executar esse código após ter concluído a Tarefa 3, onde foram verificados os valores inválidos nas colunas relevantes.

Tarefa 5: Split dos Dados em Subconjuntos de Treinamento e Teste

Nesta tarefa, você irá dividir os dados em dois subconjuntos: um para treinamento e outro para teste. Siga as instruções abaixo:

Importar a função train_test_split():
- Utilize o comando from sklearn.model_selection import train_test_split para importar a função train_test_split() da biblioteca scikit-learn.
Selecionar as características (features) e a variável alvo:
- Selecione todas as colunas do DataFrame df, exceto a coluna “Avaliacoes”, e atribua essas features a uma variável chamada X.
- Selecione apenas a coluna “Avaliacoes” do DataFrame df como uma série e atribua-a a uma variável chamada y.
Dividir os dados em subconjuntos de treinamento e teste:
- Utilize a função train_test_split() para dividir os dados em subconjuntos de treinamento e teste.
- Especifique os seguintes parâmetros:
  - X: variável contendo as features.
  - y: variável contendo a variável alvo.
  - test_size=0.2: define que 20% dos dados serão alocados para o conjunto de teste.
  - random_state=0: define uma semente fixa para reprodutibilidade dos resultados.
- Atribua os subconjuntos resultantes às variáveis X_treinamento, X_teste, y_treinamento e y_teste, respectivamente.

Tarefa 6 – Verifique se há Correlação forte entre as variáveis independentes

Objetivo: Verificar a correlação entre as features numéricas do conjunto de dados de treinamento e identificar possíveis pares de features com alta correlação.

Instruções:

Remova a coluna “Categoria” do DataFrame X_treinamento, uma vez que ela contém valores categóricos e não será incluída no cálculo da matriz de correlação. Atribua o resultado a uma nova variável chamada X_treinamento_numeric.
Converta as colunas relevantes do DataFrame X_treinamento_numeric para tipos numéricos usando a função pd.to_numeric(). As colunas a serem convertidas são: ‘No de Reviews', ‘No de Instalacoes', ‘Tamanho', ‘Preco' e ‘Dias desde a ultima Atualizacao'. Utilize o parâmetro errors='coerce' para lidar com possíveis erros de conversão.
Calcule a matriz de correlação usando o método corr() no DataFrame X_treinamento_numeric, que agora contém apenas as colunas numéricas.
Imprima a matriz de correlação resultante.
Analise a matriz de correlação e identifique pares de features com alta correlação. Considere as seguintes diretrizes:
- Coeficientes de correlação maiores que 0,7 ou menores que -0,7 indicam uma forte correlação positiva ou negativa, respectivamente.
- Pares de features com alta correlação podem sugerir redundância de informações e a possibilidade de remover uma das features.
- Considere a interpretação das correlações com base no conhecimento do domínio e na relevância das features para o problema em questão.
Documente suas observações e conclusões sobre a correlação entre as features. Caso identifique pares de features com alta correlação, discuta possíveis ações, como a remoção de uma das features ou a aplicação de técnicas de redução de dimensionalidade.

Lembre-se de que a análise da matriz de correlação é uma etapa importante na seleção de features e na compreensão das relações entre as variáveis do conjunto de dados.

Tarefa 7: Crie Gráficos de Dispersão

Utilizando o conjunto de dados de treinamento (X_treinamento_numeric) e a variável alvo de treinamento (y_treinamento), crie 5 gráficos de dispersão para visualizar a relação entre a coluna “Classificacao” e outras colunas numéricas relevantes.

Siga as etapas abaixo para criar os gráficos:

1. Selecione as colunas numéricas que você deseja plotar no eixo x dos gráficos de dispersão. As colunas sugeridas são: ‘No de Reviews', ‘No de Instalacoes', ‘Tamanho', ‘Preco' e ‘Dias desde a ultima Atualizacao'.

2. Crie uma figura com 2 linhas e 3 colunas usando a função plt.subplots(). Defina um tamanho adequado para a figura, por exemplo, (16, 10), para garantir que os gráficos sejam legíveis.

3. Adicione um título principal à figura usando a função fig.suptitle() para indicar o propósito dos gráficos.

4. Ajuste o espaçamento entre os subplots usando fig.tight_layout() para evitar sobreposição.

5. Inicie um loop for para iterar sobre as colunas selecionadas. Para cada coluna:
– Calcule a posição do subplot na matriz de eixos usando divisão inteira e resto da divisão.
– Crie um gráfico de dispersão usando a função scatter(), passando a coluna numérica atual para o eixo x e a coluna “Classificacao” para o eixo y.
– Defina um título apropriado para o subplot usando set_title(), indicando as variáveis sendo comparadas.
– Adicione rótulos aos eixos x e y usando set_xlabel() e set_ylabel(), respectivamente.

6. Após o loop, use a função plt.show() para exibir a figura com os 6 gráficos de dispersão.

Lembre-se de que o objetivo desses gráficos é visualizar a relação entre a classificação e outras variáveis numéricas do conjunto de dados de treinamento. Analise os gráficos resultantes para identificar possíveis padrões, correlações ou outliers.

Dica: Você pode usar a lista columns_to_plot para especificar as colunas numéricas que deseja plotar no eixo x dos gráficos de dispersão.

Após criar os gráficos, interprete os resultados e discuta suas observações sobre a relação entre a classificação e as outras variáveis numéricas.

Tarefa 8 – Pré-processamento de Dados

Agora, precisamos fazer alguns pré-processamentos nos dados de X_treinamento. Vimos na Tarefa 2 que a coluna “Tamanho” possui valores ausentes. Portanto, precisamos substituir esses valores ausentes pela média dessa coluna. Além disso, precisamos escalar todas as colunas numéricas em X_treinamento e codificar a coluna “Categoria” usando a codificação one-hot.

Para fazer isso, siga as etapas abaixo:

Importe as classes StandardScaler e OneHotEncoder de sklearn.preprocessing, e a classe SimpleImputer de sklearn.impute.
Declare uma variável chamada num_col e atribua a ela a lista ['No de Reviews', 'No de Instalacoes', 'Tamanho', 'Preco', 'Dias desde a ultima Atualizacao']. Essa lista armazena os nomes de todas as características numéricas.
Declare outra variável chamada cat_col e atribua a ela a lista ['Categoria'].
Agora, estamos prontos para substituir os valores ausentes na coluna “Tamanho”. Instancie um objeto SimpleImputer com strategy='mean' e atribua-o a imp.
Use imp para chamar o método fit_transform() e passe X_treinamento[num_col] para o método. Embora apenas a coluna “Tamanho” tenha valores ausentes, não há problema em passar todas as colunas numéricas para o método fit_transform(); as colunas sem valores ausentes não serão afetadas. Atribua o array resultante a tf_num.
Em seguida, instancie um objeto StandardScaler e atribua-o a scaler.
Use scaler para chamar o método fit_transform() e passe tf_num para o método; atribua o array resultante de volta a tf_num.
Instancie um objeto OneHotEncoder e atribua-o a ohe. Certifique-se de que o objeto não retorne uma matriz esparsa e que a primeira categoria seja descartada durante a codificação. Tente instanciar o objeto você mesmo, certificando-se de passar os argumentos corretos para o construtor.
Use ohe para chamar o método fit_transform() e passe X_treinamento[cat_col] para o método. Atribua o array resultante a tf_cat.
Por fim, concatene tf_num e tf_cat (que são ambos arrays NumPy) ao longo do eixo 1 e atribua o array final a X_treinamento_transformado.
Verifique se você executou corretamente as etapas acima imprimindo o valor de X_treinamento_transformado[0].

Após concluir essas etapas, você terá pré-processado os dados de treinamento, substituindo os valores ausentes na coluna “Tamanho” pela média, escalonando as colunas numéricas e codificando a coluna “Categoria” usando a codificação one-hot. O array X_treinamento_transformado conterá os dados de treinamento pré-processados prontos para serem usados em um modelo de aprendizado de máquina.

Tarefa 9 – Treinamento do Nosso Modelo

Agora que já pré-processamos os dados de treinamento, estamos prontos para treinar nosso modelo de regressão linear. Nesta tarefa, vamos importar a classe LinearRegression do scikit-learn, instanciar um objeto dessa classe e usar esse objeto para treinar o modelo com os dados de treinamento pré-processados. Depois de treinar o modelo, vamos imprimir os coeficientes e o intercepto do modelo.

Para realizar essa tarefa, siga as etapas abaixo:

1. Importe a classe LinearRegression do módulo sklearn.linear_model.

2. Instancie um objeto da classe LinearRegression e atribua-o a uma variável chamada model. Você pode fazer isso simplesmente chamando o construtor da classe sem passar nenhum argumento.

3. Use o objeto model para chamar o método fit() e passe X_treinamento_transformado e y_treinamento como argumentos para o método. O método fit() treina o modelo de regressão linear usando os dados de treinamento pré-processados (X_treinamento_transformado) e os valores alvo correspondentes (y_treinamento).

4. Após o treinamento do modelo, imprima os coeficientes do modelo acessando o atributo coef_ do objeto model. O atributo coef_ é um array NumPy que contém os coeficientes estimados para cada feature do modelo.

5. Em seguida, imprima o intercepto do modelo acessando o atributo intercept_ do objeto model. O atributo intercept_ é um valor escalar que representa o intercepto (ou termo constante) do modelo.

6. Verifique se você executou corretamente as etapas acima, certificando-se de que os coeficientes e o intercepto foram impressos corretamente.

Após concluir essas etapas, você terá treinado um modelo de regressão linear usando os dados de treinamento pré-processados. Os coeficientes e o intercepto impressos fornecem informações sobre a relação entre as features e a variável alvo, e podem ser usados para interpretar a influência de cada feature no modelo.

Lembre-se de que os coeficientes representam a mudança na variável alvo para cada unidade de mudança nas features correspondentes, mantendo todas as outras features constantes. O intercepto representa o valor previsto da variável alvo quando todas as features são zero.

Com o modelo treinado, você estará pronto para avaliar seu desempenho e fazer previsões em novos dados nas próximas tarefas.

Tarefa 10 – Avaliar o Modelo

Agora que treinamos nosso modelo de regressão linear, é hora de avaliar seu desempenho tanto no conjunto de dados de treinamento quanto no conjunto de dados de teste. Vamos usar as métricas de Raiz do Erro Quadrático Médio (RMSE) e Coeficiente de Determinação (R²) para avaliar o modelo.

Para realizar essa tarefa, siga as etapas abaixo:

1. Importe as funções mean_squared_error e r2_score do módulo sklearn.metrics.

2. Avaliação no conjunto de dados de treinamento:
– Use o objeto model para fazer previsões no conjunto de dados de treinamento transformado (X_treinamento_transformado) chamando o método predict(). Atribua as previsões a uma variável chamada y_pred_treinamento.
– Calcule o RMSE para o conjunto de treinamento usando a função mean_squared_error(). Passe y_treinamento e y_pred_treinamento como argumentos e especifique squared=False para obter a raiz quadrada do erro quadrático médio. Atribua o resultado a uma variável chamada rmse_treinamento.
– Calcule o R² para o conjunto de treinamento usando a função r2_score(). Passe y_treinamento e y_pred_treinamento como argumentos. Atribua o resultado a uma variável chamada r2_treinamento.
– Imprima os valores de rmse_treinamento e r2_treinamento para verificar o desempenho do modelo no conjunto de treinamento.

3. Avaliação no conjunto de dados de teste:
– Antes de fazer previsões no conjunto de dados de teste, precisamos aplicar as mesmas transformações que aplicamos nos dados de treinamento. Crie uma nova variável chamada X_teste_transformado e atribua a ela o resultado das seguintes etapas:
– Use o objeto imp (criado na Tarefa 8) para transformar X_teste[num_col] usando o método transform(). Atribua o resultado a tf_num_teste.
– Use o objeto scaler (criado na Tarefa 8) para transformar tf_num_teste usando o método transform(). Atribua o resultado de volta a tf_num_teste.
– Use o objeto ohe (criado na Tarefa 8) para transformar X_teste[cat_col] usando o método transform(). Atribua o resultado a tf_cat_teste.
– Concatene tf_num_teste e tf_cat_teste ao longo do eixo 1 usando np.concatenate() e atribua o resultado a X_teste_transformado.
– Use o objeto model para fazer previsões no conjunto de dados de teste transformado (X_teste_transformado) chamando o método predict(). Atribua as previsões a uma variável chamada y_pred_teste.
– Calcule o RMSE para o conjunto de teste usando a função mean_squared_error(). Passe y_teste e y_pred_teste como argumentos e especifique squared=False. Atribua o resultado a uma variável chamada rmse_teste.
– Calcule o R² para o conjunto de teste usando a função r2_score(). Passe y_teste e y_pred_teste como argumentos. Atribua o resultado a uma variável chamada r2_teste.
– Imprima os valores de rmse_teste e r2_teste para verificar o desempenho do modelo no conjunto de teste.

4. Verifique se você executou corretamente as etapas acima, certificando-se de que os valores de RMSE e R² foram calculados e impressos corretamente para os conjuntos de treinamento e teste.

Após concluir essas etapas, você terá avaliado o desempenho do modelo de regressão linear nos conjuntos de dados de treinamento e teste usando as métricas RMSE e R². Esses valores fornecem uma indicação de quão bem o modelo se ajusta aos dados e sua capacidade de generalização para novos dados.

Lembre-se de que um valor baixo de RMSE indica um menor erro nas previsões, enquanto um valor alto de R² (próximo de 1) indica uma boa qualidade de ajuste do modelo aos dados.

Com a avaliação do modelo concluída, você poderá interpretar os resultados e tirar conclusões sobre o desempenho do modelo de regressão linear nos dados fornecidos.

Tarefa 11 – Usar ColumnTransformer e Pipeline para simplificar o workflow

Nesta tarefa, vamos utilizar as classes ColumnTransformer e Pipeline do scikit-learn para simplificar o fluxo de trabalho.

Para executar essa tarefa, siga as etapas abaixo:

Importe as classes ColumnTransformer e Pipeline dos módulos sklearn.compose e sklearn.pipeline, respectivamente.
Crie um objeto Pipeline chamado num_preprocessing com os seguintes transformadores:
- Um objeto SimpleImputer para substituir os valores ausentes pela média.
- Um objeto StandardScaler para escalonar as features resultantes.
Crie um objeto ColumnTransformer chamado full_preprocessing com as seguintes transformações:
- Aplique o pipeline num_preprocessing nas colunas especificadas em num_col.
- Aplique um objeto OneHotEncoder (com sparse=False e drop=”first”) nas colunas especificadas em cat_col.
Crie um objeto Pipeline chamado final_pipeline com os seguintes passos:
- O transformador full_preprocessing para pré-processar o conjunto de dados.
- Um objeto LinearRegression para treinar o modelo.
Verifique se você criou corretamente os objetos num_preprocessing, full_preprocessing e final_pipeline.

Ao concluir essa tarefa, você terá simplificado o fluxo de trabalho de pré-processamento e treinamento do modelo usando as classes ColumnTransformer e Pipeline do scikit-learn. Isso tornará o código mais legível, modular e fácil de manter.

Tarefa 12 – Treinar o Modelo Usando Pipeline

Use o final_pipeline para treinar o modelo.

Tarefa 13 – Avalie o Modelo

Use o final_pipeline para avaliar o modelo. Tente avaliar o modelo no conjunto de treinamento usando RMSE e R² score metrics e imprima os resultados. Depois faça o mesmo para o subconjunto de testes. A ideia é só mostrar que o pipeline simplifica o workflow.

Tarefa 14 – Faça a Validação Cruzada