Introdução
Machine Learning (ML) é uma área da Inteligência Artificial que se concentra no desenvolvimento de algoritmos e modelos que permitem que os computadores aprendam e façam previsões ou decisões sem serem explicitamente programados. A biblioteca Scikit-Learn é uma das mais populares e poderosas ferramentas de ML em Python, oferecendo uma ampla gama de algoritmos e funcionalidades para tarefas de aprendizado supervisionado e não supervisionado.
Neste tutorial, usaremos o Google Colab e exploraremos alguns tópicos avançados de Machine Learning utilizando a biblioteca Scikit-Learn. Abordaremos conceitos como redução de dimensionalidade, overfitting, underfitting e ajuste de hiperparâmetros, fornecendo exemplos práticos para ilustrar esses conceitos.
Análise de Dados sem Redução de Dimensionalidade
Antes de partirmos para o tema de Redução de Dimensionalidade vamos analisar visualmente o que acontece quando não usamos a Redução de Dimensionalidade.
Aqui está um código em Python que mostra o conjunto de dados Iris sem a redução de dimensionalidade, destacando visualmente as diferentes classes de flores usando gráficos de dispersão (scatter plots) em pares de variáveis:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
from sklearn.datasets import load_iris import matplotlib.pyplot as plt import seaborn as sns # Carregando o conjunto de dados Iris iris = load_iris() X = iris.data y = iris.target # Criando um dataframe com os dados e os rótulos das classes df = sns.load_dataset('iris') # Plotando os gráficos de dispersão em pares de variáveis plt.figure(figsize=(10, 10)) sns.pairplot(df, hue='species', diag_kind='hist', markers='+', palette='husl') plt.suptitle('Conjunto de Dados Iris sem Redução de Dimensionalidade', fontsize=16) plt.show() |
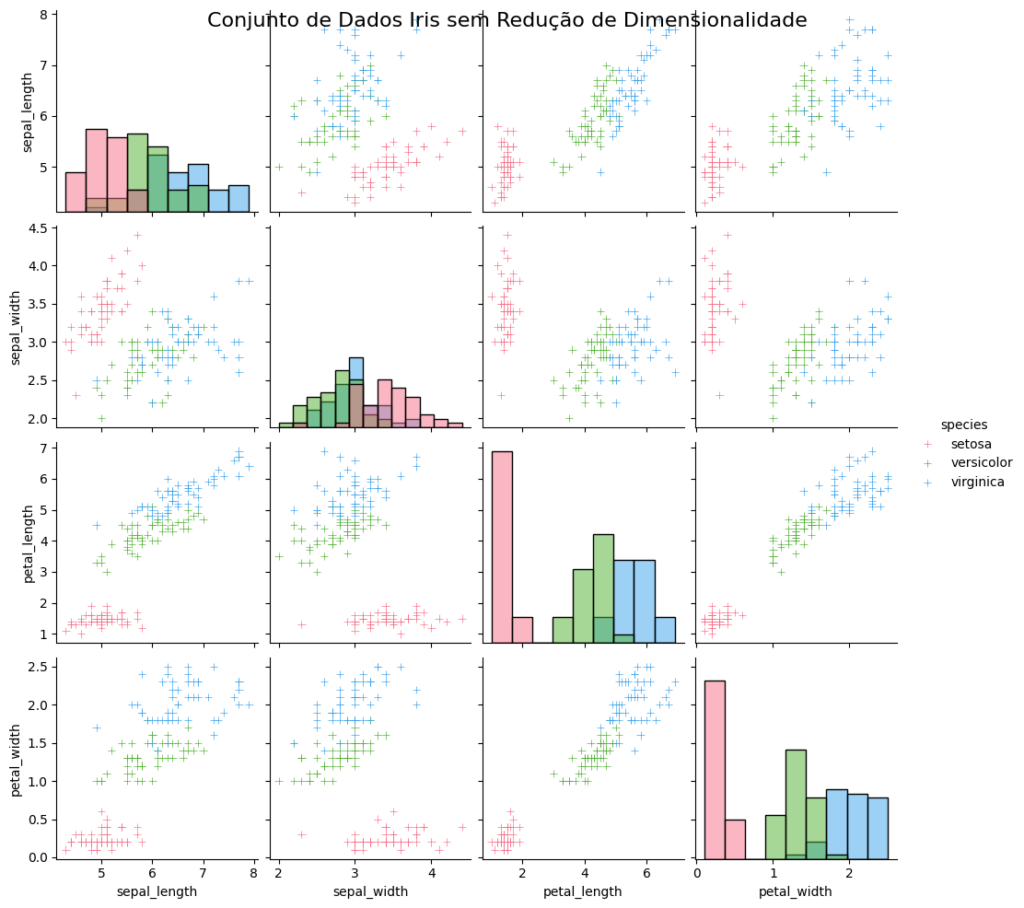
Estamos trabalhando com o conjunto de dados Iris, que contém informações sobre três espécies de flores: setosa, versicolor e virginica. Cada flor tem quatro características medidas: comprimento da sépala, largura da sépala, comprimento da pétala e largura da pétala.
Neste código:
- Carregamos o conjunto de dados Iris usando a função
load_iris()da biblioteca Scikit-Learn. - Criamos um dataframe chamado
dfusando a funçãoload_dataset('iris')da biblioteca Seaborn. Isso nos permite acessar os nomes das variáveis e das classes diretamente. - Utilizamos a função
pairplot()do Seaborn para criar uma matriz de gráficos de dispersão em pares de variáveis. Cada gráfico de dispersão mostra a relação entre duas variáveis do conjunto de dados Iris. - O parâmetro
hue='species'define a coluna que será usada para colorir os pontos de acordo com a classe da flor. - O parâmetro
diag_kind='hist'define que, na diagonal principal da matriz de gráficos, serão exibidos histogramas das variáveis individuais. - O parâmetro
markers='+'define o estilo dos marcadores usados nos gráficos de dispersão. - O parâmetro
palette='husl'define a paleta de cores usada para diferenciar as classes. - Adicionamos um título principal ao gráfico usando
plt.suptitle(). - Exibimos o gráfico usando
plt.show().
Ao executar este código, você verá uma matriz de gráficos de dispersão que mostra as relações entre as variáveis do conjunto de dados Iris. Cada gráfico de dispersão representa a relação entre duas variáveis, e os pontos são coloridos de acordo com a classe da flor (setosa, versicolor ou virginica). Na diagonal principal, são exibidos histogramas das variáveis individuais.
Esse gráfico permite visualizar o conjunto de dados Iris em seu espaço original de 4 dimensões, destacando as relações entre as variáveis e a separação entre as classes de flores. Cada classe é representada por uma cor diferente, facilitando a identificação de padrões e a distinção entre as classes.
Essa visualização sem a redução de dimensionalidade nos dá uma visão geral das relações entre as variáveis e da estrutura do conjunto de dados Iris em seu espaço original de características.
Entendendo Visualmente a Redução de Dimensionalidade
A redução de dimensionalidade é uma técnica utilizada para reduzir o número de variáveis (features) em um conjunto de dados, mantendo a maior parte da informação relevante. Isso é especialmente útil quando lidamos com conjuntos de dados de alta dimensionalidade, onde o número de variáveis é muito grande em comparação com o número de amostras.
Uma das técnicas mais comuns de redução de dimensionalidade é a PCA (Principal Component Analysis). A PCA identifica as direções (componentes principais) ao longo das quais os dados variam mais e projeta os dados nessas direções, reduzindo assim a dimensionalidade.
A PCA é uma técnica estatística que identifica as direções (componentes principais) ao longo das quais os dados variam mais. Essas direções são ortogonais (perpendiculares) entre si e representam a máxima variância nos dados.
A ideia principal da PCA é encontrar uma nova base de vetores (componentes principais) que melhor represente os dados. Esses componentes principais são combinações lineares das variáveis originais e são ordenados em ordem decrescente de variância explicada.
Existem várias razões pelas quais a redução de dimensionalidade é benéfica:
- Redução do custo computacional: Conjuntos de dados com muitas variáveis podem ser computacionalmente caros para processar e treinar modelos. Ao reduzir a dimensionalidade, podemos diminuir o tempo e os recursos necessários para treinar e aplicar os modelos.
- Visualização de dados: Quando temos muitas variáveis, é difícil visualizar os dados em um espaço de alta dimensão. A redução de dimensionalidade nos permite projetar os dados em um espaço de menor dimensão, facilitando a visualização e a compreensão dos padrões e estruturas subjacentes.
- Remoção de ruído e redundância: Algumas variáveis podem ser ruidosas ou redundantes, não contribuindo significativamente para a informação relevante. A redução de dimensionalidade pode ajudar a remover essas variáveis, concentrando-se nas características mais importantes.
O processo da PCA pode ser resumido da seguinte forma:
- Centralização dos dados: Os dados são centralizados subtraindo a média de cada variável. Isso faz com que os dados tenham média zero.
- Cálculo da matriz de covariância: A matriz de covariância é calculada para capturar as relações entre as variáveis. Ela mede como as variáveis variam em relação umas às outras.
- Decomposição em autovalores e autovetores: A matriz de covariância é decomposta em seus autovalores e autovetores correspondentes. Os autovetores representam as direções dos componentes principais, enquanto os autovalores representam a quantidade de variância explicada por cada componente principal.
- Seleção dos componentes principais: Os componentes principais são selecionados com base na quantidade de variância que explicam. Geralmente, escolhemos os componentes principais que explicam a maior parte da variância total dos dados.
- Projeção dos dados: Os dados originais são projetados no novo espaço de menor dimensão definido pelos componentes principais selecionados.
Ao aplicar a PCA, podemos reduzir a dimensionalidade dos dados, mantendo a maior parte da informação relevante. Os componentes principais selecionados capturam a maior variabilidade nos dados, permitindo uma representação mais compacta e eficiente.
É importante ressaltar que a PCA é uma técnica de redução de dimensionalidade não supervisionada, o que significa que ela não leva em consideração as variáveis de destino (labels) durante o processo de redução de dimensionalidade.
Podemos criar um código em Python usando a biblioteca Scikit-Learn para aplicar a PCA em um conjunto de dados e visualizar os resultados. Vou mostrar um exemplo usando o conjunto de dados Iris, que possui 4 variáveis (features) e 3 classes de flores.
Aqui está o código:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 |
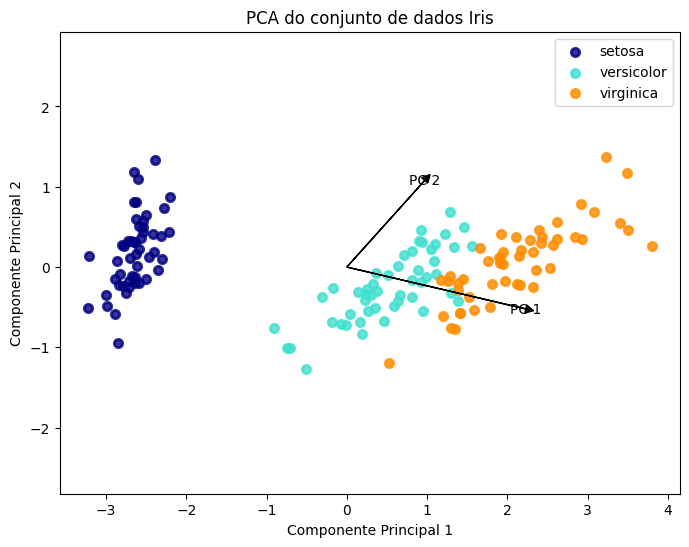
from sklearn.datasets import load_iris from sklearn.decomposition import PCA import matplotlib.pyplot as plt import numpy as np # Carregando o conjunto de dados Iris iris = load_iris() X = iris.data y = iris.target # Criando o objeto PCA com 2 componentes principais pca = PCA(n_components=2) # Aplicando a PCA nos dados X_pca = pca.fit_transform(X) # Plotando os dados transformados plt.figure(figsize=(8, 6)) colors = ['navy', 'turquoise', 'darkorange'] lw = 2 for color, i, target_name in zip(colors, [0, 1, 2], iris.target_names): plt.scatter(X_pca[y == i, 0], X_pca[y == i, 1], color=color, alpha=.8, lw=lw, label=target_name) plt.legend(loc='best', shadow=False, scatterpoints=1) plt.title('PCA do conjunto de dados Iris') plt.xlabel('Componente Principal 1') plt.ylabel('Componente Principal 2') # Plotando as direções dos componentes principais for i, (component, var) in enumerate(zip(pca.components_, pca.explained_variance_)): comp = component * 3 * np.sqrt(var) plt.arrow(0, 0, comp[0], comp[1], head_width=0.1, head_length=0.1, fc='k', ec='k') plt.annotate(f"PC {i+1}", (comp[0], comp[1]), ha='center', va='center') plt.axis('equal') plt.show() |
Neste código:
- Carregamos o conjunto de dados Iris usando a função
load_iris()da biblioteca Scikit-Learn. - Criamos um objeto PCA com 2 componentes principais usando
PCA(n_components=2). Isso reduzirá a dimensionalidade dos dados de 4 para 2. - Aplicamos a PCA nos dados usando o método
fit_transform(), que ajusta a PCA aos dados e retorna os dados transformados. - Plotamos os dados transformados usando a função
scatter()do Matplotlib. Cada classe de flor é representada por uma cor diferente. - Adicionamos uma legenda e rótulos aos eixos para melhorar a interpretação do gráfico.
- Plotamos as direções dos componentes principais usando a função
arrow()do Matplotlib. As direções são calculadas multiplicando os componentes principais pela raiz quadrada da variância explicada e por um fator de escala (3, neste caso). - Anotamos os rótulos dos componentes principais usando a função
annotate()do Matplotlib. - Definimos a escala dos eixos como igual usando
plt.axis('equal')para manter a proporção correta. - Exibimos o gráfico usando
plt.show().
Ao executar este código, você verá um gráfico que mostra os dados do conjunto Iris projetados nos dois componentes principais. Cada ponto representa uma amostra, e as cores representam as diferentes classes de flores. As setas indicam as direções dos componentes principais.
Assim como no exemplo anterior, estamos trabalhando com o conjunto de dados Iris, que contém informações sobre três espécies de flores: setosa, versicolor e virginica. Cada flor tem quatro características medidas: comprimento da sépala, largura da sépala, comprimento da pétala e largura da pétala.
Quando você executa esse código, ele cria um gráfico de dispersão que mostra os dados do conjunto Iris após a aplicação da PCA. Cada ponto representa uma flor, e as cores representam as diferentes espécies. As setas indicam as direções dos componentes principais.
A PCA é uma técnica que reduz a dimensionalidade dos dados, transformando-os em um novo espaço de características com menos dimensões, mantendo a maior parte da informação relevante. Nesse caso, reduzimos as 4 características originais para 2 componentes principais.
Essa visualização com a PCA nos permite ver como as diferentes espécies de flores se agrupam e se diferenciam no novo espaço de características reduzido. Podemos observar se as espécies formam grupos distintos ou se há sobreposição entre elas.
Em resumo, esse código carrega o conjunto de dados Iris, aplica a PCA para reduzir a dimensionalidade dos dados e cria um gráfico de dispersão para visualizar os dados transformados, destacando as diferentes espécies de flores com cores distintas e mostrando as direções dos componentes principais.
Esse exemplo visual ajuda a entender como a PCA reduz a dimensionalidade dos dados, projetando-os em um espaço de menor dimensão, mantendo a maior parte da variância explicada.
Exemplo de Redução de Dimensionalidade utilizando Scikit-Learn:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
from sklearn.decomposition import PCA from sklearn.datasets import load_iris # Carregando o conjunto de dados Iris iris = load_iris() X = iris.data # Criando o objeto PCA com 2 componentes pca = PCA(n_components=2) # Aplicando a redução de dimensionalidade X_reduced = pca.fit_transform(X) # Visualizando os dados reduzidos import matplotlib.pyplot as plt plt.scatter(X_reduced[:, 0], X_reduced[:, 1], c=iris.target) plt.xlabel('Componente Principal 1') plt.ylabel('Componente Principal 2') plt.title('Redução de Dimensionalidade com PCA') plt.show() |
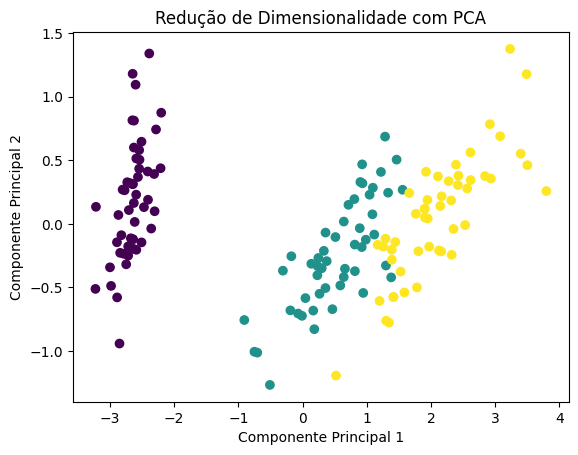
A diferença fundamental ao aplicar a PCA (Principal Component Analysis) em um conjunto de dados é a redução da dimensionalidade, ou seja, a redução do número de variáveis (features) mantendo a maior parte da informação relevante.
No caso do conjunto de dados Iris, temos originalmente 4 variáveis (features) para cada amostra:
1. Comprimento da sépala (sepal length)
2. Largura da sépala (sepal width)
3. Comprimento da pétala (petal length)
4. Largura da pétala (petal width)
Cada amostra no conjunto de dados Iris é representada por essas 4 variáveis. Portanto, sem a redução de dimensionalidade, estamos lidando com um espaço de características de 4 dimensões.
Ao aplicar a PCA com 2 componentes principais, estamos reduzindo a dimensionalidade dos dados de 4 para 2. Isso significa que cada amostra agora será representada por apenas 2 variáveis (os componentes principais) em vez das 4 variáveis originais.
A PCA encontra as direções (componentes principais) ao longo das quais os dados variam mais. Essas direções são combinações lineares das variáveis originais e são ordenadas em ordem decrescente de variância explicada. Os componentes principais são ortogonais (perpendiculares) entre si.
Portanto, após a aplicação da PCA, cada amostra no conjunto de dados Iris será representada por 2 novos valores, que são as projeções das amostras nos 2 componentes principais selecionados. Esses componentes principais capturam a maior parte da variância presente nos dados originais.
A vantagem da redução de dimensionalidade com a PCA é que podemos representar os dados em um espaço de menor dimensão, mantendo a maior parte da informação relevante. Isso pode ser útil para visualização, pois é mais fácil visualizar dados em 2 ou 3 dimensões do que em 4 dimensões. Além disso, a redução de dimensionalidade pode ajudar a reduzir o custo computacional e a complexidade dos modelos de aprendizado de máquina, pois eles lidarão com menos variáveis.
No entanto, é importante ressaltar que a PCA é uma técnica de redução de dimensionalidade não supervisionada, o que significa que ela não leva em consideração as variáveis de destino (labels) durante o processo. A PCA busca capturar a variância nos dados, independentemente das classes ou rótulos associados a cada amostra.
Em resumo, a diferença fundamental ao aplicar a PCA no conjunto de dados Iris é que passamos de um espaço de características de 4 dimensões para um espaço de 2 dimensões, mantendo a maior parte da variância presente nos dados originais. Isso pode facilitar a visualização e a análise dos dados, além de potencialmente reduzir a complexidade computacional em tarefas subsequentes de aprendizado de máquina.
Overfitting
Overfitting e underfitting são problemas comuns em Machine Learning que afetam a capacidade de generalização dos modelos. Overfitting ocorre quando um modelo se ajusta muito bem aos dados de treinamento, capturando até mesmo o ruído e as flutuações aleatórias. Isso resulta em um desempenho ruim em dados não vistos.
Imagine que você está tentando ensinar um modelo de aprendizado de máquina a reconhecer diferentes tipos de frutas com base em suas características, como cor, tamanho e forma. Você tem um conjunto de dados de treinamento com exemplos de frutas e suas respectivas etiquetas (maçã, banana, laranja, etc.).
Imagine que você tem um modelo complexo com muitos parâmetros e o treina com um conjunto de dados pequeno. O modelo pode acabar memorizando perfeitamente os exemplos de treinamento, incluindo detalhes específicos e ruídos, mas falha em generalizar para novos exemplos.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 |
import numpy as np import matplotlib.pyplot as plt # Gerando dados de exemplo np.random.seed(42) X = np.sort(5 * np.random.rand(40, 1), axis=0) y = np.sin(X).ravel() y[::5] += 3 * (0.5 - np.random.rand(8)) # Criando o modelo de overfitting from sklearn.pipeline import make_pipeline from sklearn.preprocessing import PolynomialFeatures from sklearn.linear_model import LinearRegression degree = 15 model = make_pipeline(PolynomialFeatures(degree), LinearRegression()) model.fit(X, y) # Plotando os dados e o modelo X_plot = np.linspace(0, 5, 100)[:, np.newaxis] y_plot = model.predict(X_plot) plt.figure(figsize=(8, 6)) plt.scatter(X, y, color='red', label='Dados de Treinamento') plt.plot(X_plot, y_plot, color='blue', linewidth=2, label='Modelo com Overfitting') plt.xlabel('X') plt.ylabel('y') plt.legend() plt.title('Exemplo de Overfitting') plt.show() |
Exemplo visual de overfitting:
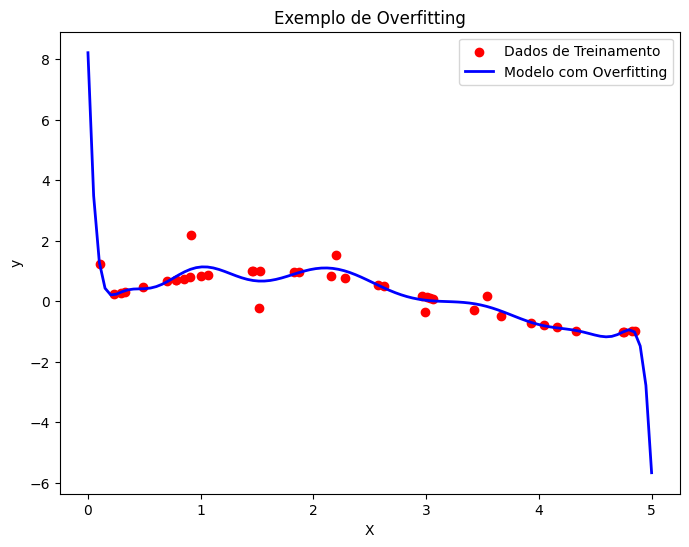
No gráfico acima, a linha azul representa o modelo com overfitting. Ele se ajusta perfeitamente aos pontos de dados de treinamento (pontos vermelhos), mas falha em capturar a tendência geral dos dados. Quando novos dados são apresentados, o modelo não consegue fazer previsões precisas.
Como Lidar com o Overfitting
Para lidar com overfitting, podemos utilizar técnicas como regularização e validação cruzada. A regularização adiciona um termo de penalidade à função de perda do modelo, restringindo a complexidade do modelo. A validação cruzada nos ajuda a avaliar o desempenho do modelo em dados não vistos.
Exemplo utilizando Scikit-Learn (Você precisa carregar o arquivo “cal_housing.data”):
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 |
import numpy as np import matplotlib.pyplot as plt from sklearn.linear_model import Ridge, LinearRegression from sklearn.model_selection import train_test_split, cross_val_score # Carregando o conjunto de dados California Housing data = np.loadtxt('cal_housing.data', delimiter=',') X, y = data[:, :-1], data[:, -1] # Dividindo os dados em conjuntos de treinamento e teste X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42) # Criando os modelos de regressão com diferentes valores de alpha alphas = [0.1, 1.0, 10.0] ridge_models = [Ridge(alpha=a) for a in alphas] linear_model = LinearRegression() # Calculando os scores de validação cruzada para cada modelo cv_scores_ridge = [cross_val_score(model, X_train, y_train, cv=5).mean() for model in ridge_models] cv_score_linear = cross_val_score(linear_model, X_train, y_train, cv=5).mean() # Treinando os modelos for model in ridge_models: model.fit(X_train, y_train) linear_model.fit(X_train, y_train) # Calculando os scores de treinamento e teste para cada modelo train_scores_ridge = [model.score(X_train, y_train) for model in ridge_models] test_scores_ridge = [model.score(X_test, y_test) for model in ridge_models] train_score_linear = linear_model.score(X_train, y_train) test_score_linear = linear_model.score(X_test, y_test) # Imprimindo os scores de treinamento e teste print("Scores de Treinamento (Ridge):", train_scores_ridge) print("Scores de Teste (Ridge):", test_scores_ridge) print("Score de Treinamento (Linear):", train_score_linear) print("Score de Teste (Linear):", test_score_linear) # Fazendo previsões nos conjuntos de teste y_test_pred_ridge = [model.predict(X_test) for model in ridge_models] y_test_pred_linear = linear_model.predict(X_test) # Plotando os resultados plt.figure(figsize=(12, 6)) # Gráfico dos scores de validação cruzada plt.subplot(1, 2, 1) plt.plot(alphas, cv_scores_ridge, marker='o', label='Ridge') plt.axhline(cv_score_linear, color='red', linestyle='--', label='Linear') plt.xscale('log') plt.xlabel('Alpha') plt.ylabel('Score de Validação Cruzada') plt.title('Scores de Validação Cruzada') plt.legend() plt.grid(True) # Gráfico das previsões no conjunto de teste plt.subplot(1, 2, 2) for i, alpha in enumerate(alphas): plt.scatter(y_test, y_test_pred_ridge[i], alpha=0.5, label=f'Ridge (alpha={alpha})') plt.scatter(y_test, y_test_pred_linear, color='red', alpha=0.5, label='Linear') plt.plot([0, 5], [0, 5], color='black', linestyle='--') plt.xlabel('Valores Reais') plt.ylabel('Previsões') plt.title('Previsões no Conjunto de Teste') plt.legend() plt.grid(True) plt.tight_layout() plt.show() |
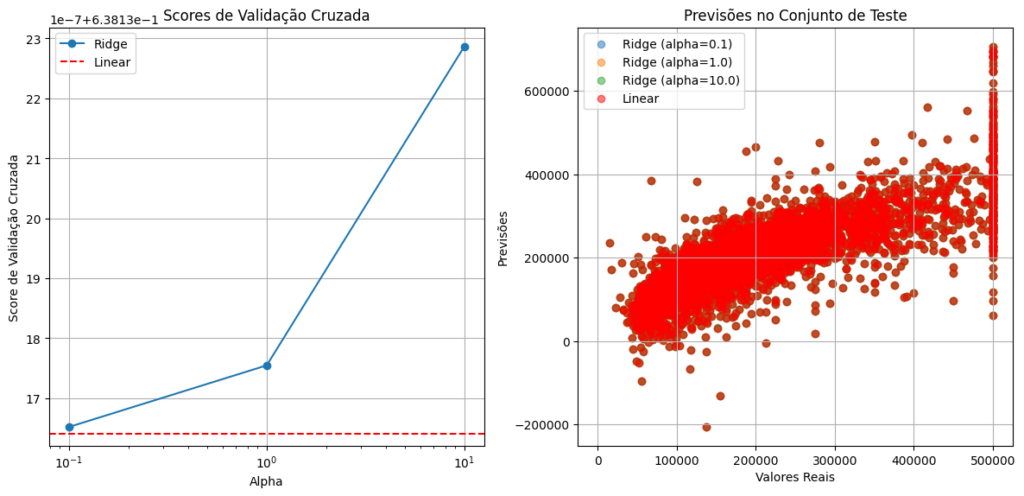
- Gráfico dos Scores de Validação Cruzada:
- O eixo x representa os diferentes valores de
alphausados na regressão Ridge. Oalphaé o parâmetro de regularização que controla a intensidade da regularização aplicada ao modelo. - O eixo y representa os scores de validação cruzada, que medem o desempenho do modelo em dados não vistos durante o treinamento.
- A linha azul representa os scores de validação cruzada para o modelo Ridge com diferentes valores de
alpha. Quanto maior o valor dealpha, maior a regularização aplicada. - A linha vermelha tracejada representa o score de validação cruzada para o modelo linear (sem regularização).
- Ao observar esse gráfico, você pode ver como o desempenho do modelo Ridge varia com diferentes níveis de regularização. Se o score de validação cruzada for maior para um determinado valor de
alpha, isso indica que esse nível de regularização é mais eficaz na redução do overfitting. - Você também pode comparar os scores do modelo Ridge com o modelo linear. Se o modelo Ridge tiver scores mais altos, isso sugere que a regularização está ajudando a melhorar o desempenho em comparação com o modelo não regularizado.
- O eixo x representa os diferentes valores de
- Gráfico das Previsões no Conjunto de Teste:
- O eixo x representa os valores reais do conjunto de teste.
- O eixo y representa as previsões feitas pelos modelos para o conjunto de teste.
- Os pontos coloridos representam as previsões feitas pelos modelos Ridge com diferentes valores de
alpha. Cada cor corresponde a um valor específico dealpha. - Os pontos vermelhos representam as previsões feitas pelo modelo linear.
- A linha preta tracejada representa a linha de referência, onde as previsões perfeitas coincidiriam com os valores reais.
- Ao observar esse gráfico, você pode ver como as previsões dos modelos se comparam com os valores reais. Se os pontos estiverem mais próximos da linha de referência, isso indica que o modelo está fazendo previsões mais precisas.
- Você pode comparar as previsões dos modelos Ridge com diferentes níveis de regularização. Se os pontos de um modelo Ridge estiverem mais próximos da linha de referência em comparação com outros modelos Ridge ou com o modelo linear, isso sugere que esse nível de regularização está ajudando a reduzir o overfitting e melhorar a capacidade de generalização do modelo.
Em resumo, o gráfico dos scores de validação cruzada permite avaliar o desempenho dos modelos em dados não vistos e comparar os efeitos de diferentes níveis de regularização. O gráfico das previsões no conjunto de teste permite visualizar a qualidade das previsões dos modelos em relação aos valores reais e comparar o desempenho dos modelos Ridge com diferentes níveis de regularização e do modelo linear.
Ao analisar esses gráficos, você pode obter insights sobre como a regularização está impactando o desempenho do modelo e qual nível de regularização é mais eficaz na redução do overfitting. Isso pode ajudar na seleção do melhor modelo e na compreensão dos benefícios da regularização no tratamento do overfitting.
Undefitting
Underfitting ocorre quando um modelo é muito simples e não captura adequadamente os padrões subjacentes nos dados de treinamento, resultando em um desempenho ruim tanto nos dados de treinamento quanto nos dados de teste.
Imagine que você tem um modelo muito simples, como uma linha reta, para tentar ajustar dados complexos e não lineares. O modelo não será capaz de capturar a complexidade dos dados e terá um desempenho ruim tanto nos dados de treinamento quanto nos dados de teste.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 |
import numpy as np import matplotlib.pyplot as plt # Gerando dados de exemplo np.random.seed(42) X = np.sort(5 * np.random.rand(40, 1), axis=0) y = np.sin(X).ravel() y[::5] += 3 * (0.5 - np.random.rand(8)) # Criando o modelo de underfitting from sklearn.linear_model import LinearRegression model = LinearRegression() model.fit(X, y) # Plotando os dados e o modelo X_plot = np.linspace(0, 5, 100)[:, np.newaxis] y_plot = model.predict(X_plot) plt.figure(figsize=(8, 6)) plt.scatter(X, y, color='red', label='Dados de Treinamento') plt.plot(X_plot, y_plot, color='green', linewidth=2, label='Modelo com Underfitting') plt.xlabel('X') plt.ylabel('y') plt.legend() plt.title('Exemplo de Underfitting') plt.show() |
Exemplo visual de underfitting:
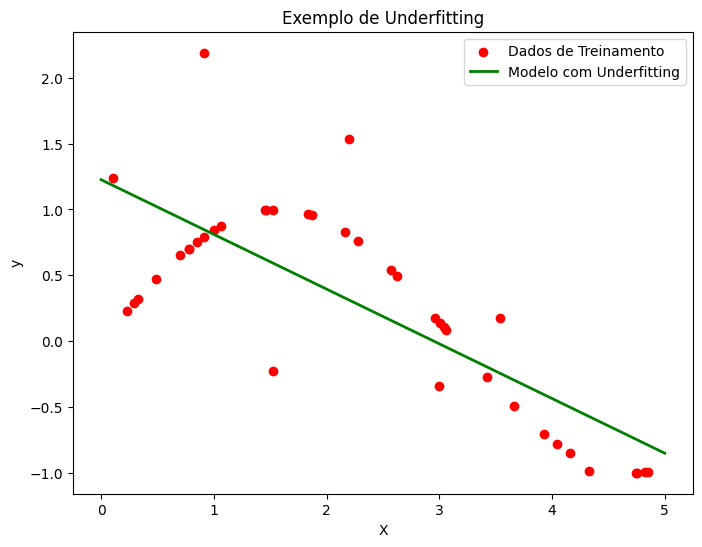
O gráfico de underfitting ilustra um modelo que é muito simples para capturar a complexidade dos dados. Vamos analisar os principais elementos do gráfico:
- Dados de Treinamento (pontos vermelhos):
- Os pontos vermelhos representam os dados de treinamento, ou seja, os dados reais que foram usados para treinar o modelo.
- Esses pontos mostram a relação entre a variável independente (X) e a variável dependente (y).
- Neste exemplo, os dados de treinamento parecem seguir um padrão não linear, com algumas flutuações aleatórias.
- Modelo com Underfitting (linha verde):
- A linha verde representa o modelo de regressão linear ajustado aos dados de treinamento.
- No caso de underfitting, o modelo é muito simples e não consegue capturar a complexidade dos dados.
- Neste exemplo, o modelo de regressão linear é uma linha reta que não se ajusta bem aos dados de treinamento.
- O modelo com underfitting tende a ter um alto viés (bias), ou seja, ele faz suposições simplistas sobre a relação entre X e y.
- Eixos X e Y:
- O eixo X representa a variável independente (X), que é usada para fazer previsões.
- O eixo Y representa a variável dependente (y), que é a variável que estamos tentando prever.
Ao interpretar o gráfico, podemos observar o seguinte:
- O modelo de regressão linear (linha verde) não se ajusta bem aos dados de treinamento (pontos vermelhos). Ele é uma aproximação muito simplista da relação entre X e y.
- O modelo com underfitting não captura a não linearidade presente nos dados. Ele assume uma relação linear, enquanto os dados claramente seguem um padrão não linear.
- Como resultado, o modelo com underfitting terá um desempenho ruim tanto nos dados de treinamento quanto em novos dados, pois não é capaz de generalizar bem.
- A diferença entre as previsões do modelo (linha verde) e os dados reais (pontos vermelhos) é grande, indicando um alto erro de previsão.
O underfitting ocorre quando o modelo é muito simples para representar a complexidade dos dados. Isso pode acontecer quando:
- O modelo escolhido é inadequado para o problema em questão (por exemplo, usar regressão linear para dados não lineares).
- O modelo não tem parâmetros suficientes para capturar os padrões nos dados.
- Os dados de treinamento são insuficientes para o modelo aprender adequadamente.
Em resumo, o gráfico de underfitting mostra um modelo que é muito simples para capturar a complexidade dos dados, resultando em um alto erro de previsão e baixa capacidade de generalização.
Usar modelos de regularização e validação cruzada é uma abordagem mais robusta para lidar com o underfitting e evitar o overfitting. A regularização adiciona um termo de penalidade à função de perda do modelo, controlando a complexidade do modelo, enquanto a validação cruzada nos ajuda a avaliar o desempenho do modelo em dados não vistos.
Aqui está um exemplo de código que utiliza a regressão polinomial com regularização (Ridge) e validação cruzada para lidar com o underfitting:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 |
import numpy as np import matplotlib.pyplot as plt from sklearn.linear_model import Ridge from sklearn.preprocessing import PolynomialFeatures from sklearn.model_selection import cross_val_score # Gerando dados de exemplo np.random.seed(42) X = np.sort(5 * np.random.rand(40, 1), axis=0) y = np.sin(X).ravel() y[::5] += 3 * (0.5 - np.random.rand(8)) # Criando e ajustando o modelo de regressão polinomial com regularização poly_features = PolynomialFeatures(degree=4, include_bias=False) X_poly = poly_features.fit_transform(X) model_poly_reg = Ridge(alpha=1.0) # Avaliando o modelo usando validação cruzada cv_scores = cross_val_score(model_poly_reg, X_poly, y, cv=5) print("Scores da validação cruzada:", cv_scores) print("Média dos scores da validação cruzada:", np.mean(cv_scores)) # Ajustando o modelo aos dados model_poly_reg.fit(X_poly, y) # Plotando os dados, o modelo original e o modelo polinomial com regularização X_plot = np.linspace(0, 5, 100)[:, np.newaxis] X_plot_poly = poly_features.transform(X_plot) y_plot_poly_reg = model_poly_reg.predict(X_plot_poly) plt.figure(figsize=(8, 6)) plt.scatter(X, y, color='red', label='Dados de Treinamento') plt.plot(X_plot, y_plot_poly_reg, color='blue', linewidth=2, label='Modelo Polinomial com Regularização') plt.xlabel('X') plt.ylabel('y') plt.legend() plt.title('Regressão Polinomial com Regularização e Validação Cruzada') plt.show() |
|
1 2 |
Scores da validação cruzada: [-1.91355624 -0.08829636 -0.82351932 -0.19997264 0.42722734] Média dos scores da validação cruzada: -0.5196234427977773 |
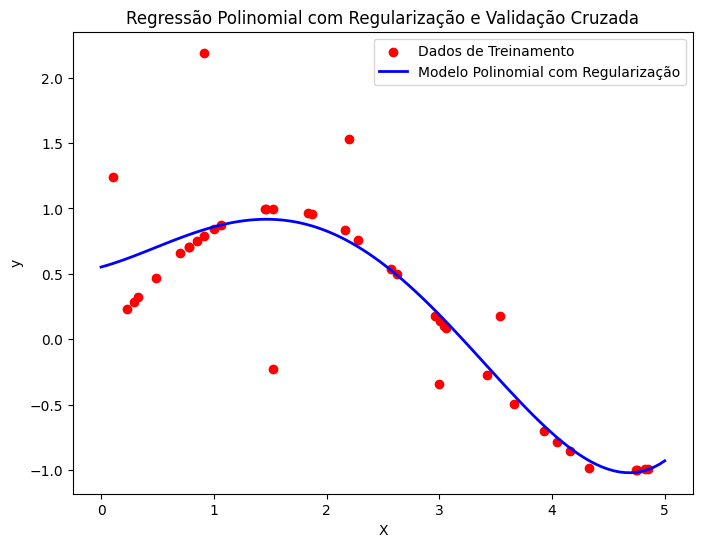
Neste código:
- Usamos os mesmos dados de exemplo do código anterior.
- Criamos um objeto
PolynomialFeaturespara gerar características polinomiais de grau 4. - Criamos um objeto
Ridgedo Scikit-Learn, que é um modelo de regressão linear com regularização L2 (Ridge). O parâmetroalphacontrola a força da regularização. Quanto maior o valor dealpha, maior a penalidade aplicada aos coeficientes do modelo. - Utilizamos a função
cross_val_scoredo Scikit-Learn para avaliar o desempenho do modelo usando validação cruzada. Definimos o número de folds como 5 (cv=5). A função retorna os scores de cada fold da validação cruzada. - Imprimimos os scores da validação cruzada e a média desses scores para ter uma estimativa do desempenho do modelo.
- Ajustamos o modelo aos dados usando
model_poly_reg.fit(X_poly, y). - Plotamos os dados de treinamento como pontos vermelhos e o modelo polinomial com regularização como uma linha azul.
Ao executar esse código, você verá os scores da validação cruzada impressos no console e um gráfico mostrando o modelo polinomial com regularização ajustado aos dados.
A regularização ajuda a controlar a complexidade do modelo, evitando que ele se ajuste excessivamente aos dados de treinamento. A validação cruzada nos fornece uma estimativa mais confiável do desempenho do modelo em dados não vistos, ajudando a evitar o overfitting.
É importante notar que a escolha do valor de alpha na regularização pode afetar o desempenho do modelo. Valores muito altos de alpha podem levar a underfitting, enquanto valores muito baixos podem não ser eficazes na prevenção do overfitting. A validação cruzada pode ser usada para ajudar a selecionar um valor apropriado de alpha.
Ajuste de Hiperparâmetros (Hyperparameter Tuning)
Os hiperparâmetros são parâmetros que não são aprendidos durante o treinamento do modelo, mas sim definidos antes do treinamento. O ajuste de hiperparâmetros é o processo de encontrar a melhor combinação de hiperparâmetros que maximiza o desempenho do modelo.
Duas técnicas comuns para o ajuste de hiperparâmetros são Grid Search e Random Search. Grid Search testa todas as combinações possíveis de hiperparâmetros especificados, enquanto Random Search amostra aleatoriamente um número fixo de combinações de hiperparâmetros.
Exemplo utilizando Scikit-Learn:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 |
from sklearn.datasets import load_iris from sklearn.model_selection import train_test_split, GridSearchCV from sklearn.svm import SVC from sklearn.metrics import accuracy_score # Carregando o conjunto de dados Iris iris = load_iris() X = iris.data y = iris.target # Dividindo os dados em conjuntos de treinamento e teste X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42) # Criando o modelo SVM svm = SVC() # Definindo os hiperparâmetros a serem testados param_grid = { 'C': [0.1, 1, 10], 'kernel': ['linear', 'rbf'], 'gamma': [0.1, 1, 10] } # Realizando o Grid Search grid_search = GridSearchCV(svm, param_grid, cv=5) grid_search.fit(X_train, y_train) # Obtendo os melhores hiperparâmetros best_params = grid_search.best_params_ print("Melhores hiperparâmetros:", best_params) # Treinando o modelo com os melhores hiperparâmetros best_svm = SVC(**best_params) best_svm.fit(X_train, y_train) # Fazendo previsões no conjunto de teste y_pred = best_svm.predict(X_test) # Calculando a acurácia do modelo accuracy = accuracy_score(y_test, y_pred) print("Acurácia do modelo:", accuracy) |
Neste exemplo:
- Carregamos o conjunto de dados Iris usando a função
load_iris()do Scikit-Learn. - Dividimos os dados em conjuntos de treinamento e teste usando a função
train_test_split(). Isso nos permite avaliar o desempenho do modelo em dados não vistos. - Criamos um modelo SVM (Support Vector Machine) usando a classe
SVCdo Scikit-Learn. - Definimos um dicionário chamado
param_gridque especifica os hiperparâmetros a serem testados. Neste exemplo, estamos testando diferentes valores para os hiperparâmetrosC(parâmetro de regularização),kernel(tipo de kernel) egamma(coeficiente do kernel). - Realizamos o Grid Search usando a classe
GridSearchCVdo Scikit-Learn. Especificamos o modelo SVM, oparam_gride o número de folds para a validação cruzada (cv=5). - Ajustamos o Grid Search aos dados de treinamento usando o método
fit(). - Obtemos os melhores hiperparâmetros encontrados pelo Grid Search acessando o atributo
best_params_. - Criamos um novo modelo SVM com os melhores hiperparâmetros encontrados e o treinamos nos dados de treinamento.
- Fazemos previsões no conjunto de teste usando o método
predict()e calculamos a acurácia do modelo usando a funçãoaccuracy_score()do Scikit-Learn.
Ao executar esse código, você verá os melhores hiperparâmetros encontrados pelo Grid Search e a acurácia do modelo nos dados de teste.
Saída:
|
1 2 |
Melhores hiperparâmetros: {'C': 1, 'gamma': 0.1, 'kernel': 'linear'} Acurácia do modelo: 1.0 |
Vamos analisar cada parte da saída:
Melhores hiperparâmetros: {'C': 1, 'gamma': 0.1, 'kernel': 'linear'}- Essa linha indica os melhores valores de hiperparâmetros encontrados pelo Grid Search.
'C': 1significa que o melhor valor encontrado para o hiperparâmetroC(parâmetro de regularização) é 1. O parâmetroCcontrola a penalidade aplicada aos erros de classificação. Um valor maior deCindica uma margem mais estreita e uma penalidade maior para erros de classificação.'gamma': 0.1significa que o melhor valor encontrado para o hiperparâmetrogamma(coeficiente do kernel) é 0.1. O parâmetrogammadefine a influência de um único exemplo de treinamento. Um valor menor degammaindica uma influência mais ampla, enquanto um valor maior indica uma influência mais restrita.'kernel': 'linear'significa que o melhor tipo de kernel encontrado é o kernel linear. O kernel é uma função que transforma os dados de entrada para um espaço de características de maior dimensão, onde os dados podem ser separados linearmente.
Acurácia do modelo: 1.0- Essa linha indica a acurácia do modelo treinado com os melhores hiperparâmetros encontrados.
- A acurácia é uma métrica que mede a proporção de previsões corretas feitas pelo modelo em relação ao total de previsões.
- Uma acurácia de 1.0 significa que o modelo classificou corretamente todas as amostras do conjunto de teste. Em outras palavras, o modelo obteve um desempenho perfeito nos dados de teste.
No exemplo dado, o Grid Search encontrou que a melhor combinação de hiperparâmetros para o modelo SVM no conjunto de dados Iris é:
Cigual a 1gammaigual a 0.1kerneldo tipo linear
Com esses hiperparâmetros, o modelo treinado alcançou uma acurácia de 100% no conjunto de teste, o que indica um desempenho excepcional.
É importante ressaltar que uma acurácia de 1.0 é um resultado muito bom e pode sugerir que o modelo está se ajustando perfeitamente aos dados. No entanto, é sempre recomendado avaliar o modelo em um conjunto de dados de validação separado para verificar se ele generaliza bem para dados não vistos e não está sofrendo de overfitting (ajuste excessivo aos dados de treinamento).
O Grid Search testa todas as combinações possíveis de hiperparâmetros especificados em param_grid. Isso pode ser computacionalmente caro, especialmente se houver muitos hiperparâmetros e valores a serem testados. Uma alternativa é usar o Random Search, que amostra aleatoriamente um número fixo de combinações de hiperparâmetros.
O ajuste de hiperparâmetros é uma etapa importante para otimizar o desempenho do modelo. Ele nos permite encontrar a melhor configuração de hiperparâmetros que se ajusta bem aos dados e generaliza para dados não vistos.
Conclusão
Neste tutorial, exploramos alguns tópicos avançados de Machine Learning utilizando a biblioteca Scikit-Learn. Aprendemos sobre redução de dimensionalidade com PCA, overfitting e underfitting, e ajuste de hiperparâmetros com Grid Search e Random Search.
Esses conceitos são fundamentais para desenvolver modelos de Machine Learning robustos e eficientes. A redução de dimensionalidade nos ajuda a lidar com conjuntos de dados de alta dimensionalidade, enquanto o ajuste de hiperparâmetros nos permite encontrar a melhor configuração para nossos modelos.
A biblioteca Scikit-Learn oferece uma ampla gama de algoritmos e ferramentas para implementar esses conceitos de forma prática. Com os exemplos fornecidos neste tutorial, você pode explorar ainda mais esses tópicos e aplicá-los em seus próprios projetos de Machine Learning.
Lembre-se de que a prática é essencial para dominar esses conceitos. Experimente diferentes técnicas, ajuste hiperparâmetros e avalie o desempenho dos seus modelos em diferentes conjuntos de dados. Com dedicação e prática, você estará no caminho certo para se tornar um especialista em Machine Learning.
Espero que este tutorial tenha sido útil para você. Continue explorando e aprendendo! Se tiver alguma dúvida, não hesite em perguntar. Boa sorte em sua jornada de aprendizado de Machine Learning!