Machine Learning: Algoritmos de Classificação com Python Scikit-Learn
Introdução
Bem-vindo ao fascinante mundo do Machine Learning! Neste tutorial, exploraremos alguns dos algoritmos de classificação mais populares e aprenderemos como implementá-los usando a biblioteca Scikit-Learn do Python. Seja você um iniciante em Machine Learning com pouca experiência em programação ou alguém com conhecimento prévio em Python, este tutorial o guiará passo a passo através dos conceitos fundamentais e das aplicações práticas dos algoritmos de classificação.
Importante: Esse tutorial esta usando o Jupyter Notebooks com o Google Colab para implementação dos algoritmos. É possível utilizar o Jupyter Notebooks com Anaconda.
O que são Algoritmos de Classificação?
Os algoritmos de classificação são uma categoria de algoritmos de Machine Learning supervisionado que têm como objetivo atribuir rótulos ou classes a novos dados com base em um conjunto de dados de treinamento. Esses algoritmos aprendem padrões e características dos dados rotulados e usam esse conhecimento para fazer previsões sobre dados não vistos anteriormente.
Os algoritmos de classificação são amplamente utilizados em várias áreas, como detecção de spam em e-mails, diagnóstico médico, reconhecimento de imagem e muito mais. Eles desempenham um papel crucial na tomada de decisões automatizadas e na extração de insights valiosos a partir dos dados.
Aprenda Machine Learning em 5 Dias. Curso 100% Prático.
Melhor Preço por Tempo Limitado. Clique Aqui e Teste Sem Risco.
30 Dias de Satisfação Garantida!
Decision Tree (Árvore de Decisão)
A Decision Tree é um algoritmo de classificação que constrói uma estrutura de árvore para tomar decisões com base nos atributos dos dados. Cada nó interno da árvore representa um teste em um atributo, cada ramo representa o resultado desse teste, e cada nó folha representa uma classe ou rótulo.
Aqui está uma tabela de dados fictícios representando informações sobre a qualidade do sono, com três colunas de atributos e uma coluna de classe. O objetivo é classificar a qualidade do sono em três categorias: “Boa”, “Regular” ou “Ruim”.
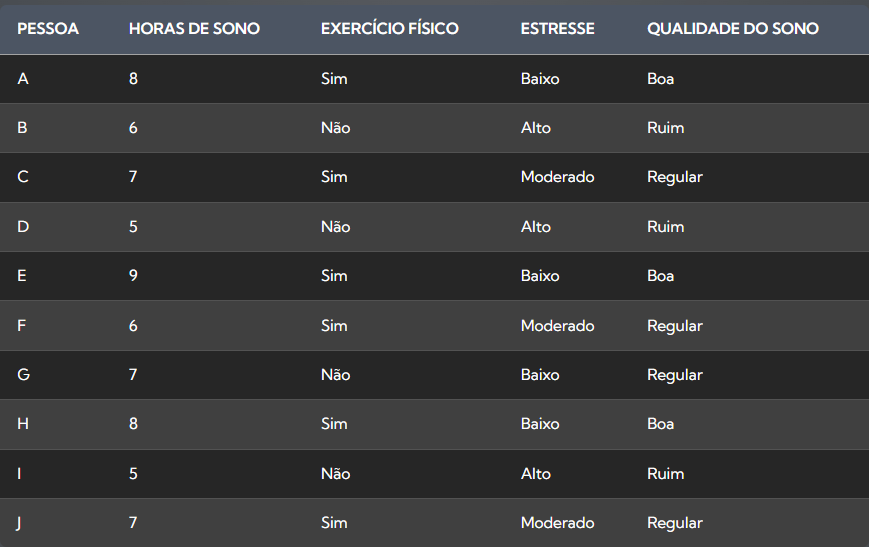
Neste exemplo, temos três atributos que podem influenciar a qualidade do sono:
- Horas de Sono: Representa a quantidade de horas que a pessoa dorme por noite.
- Exercício Físico: Indica se a pessoa pratica exercícios físicos regularmente (Sim ou Não).
- Estresse: Descreve o nível de estresse da pessoa (Baixo, Moderado ou Alto).
A coluna “Qualidade do Sono” representa a classe que queremos prever com base nos atributos. Neste caso, temos três classes possíveis: “Boa”, “Regular” ou “Ruim”.
Usando essa tabela de dados fictícios, podemos treinar uma Decision Tree para aprender os padrões e relações entre os atributos e a qualidade do sono. A árvore de decisão resultante pode ser usada para classificar a qualidade do sono de novas pessoas com base em suas horas de sono, prática de exercícios físicos e nível de estresse.
Vamos explorar algumas regras que poderiam ser aplicadas ao conjunto de dados de acordo com o peso e o Gini Impurity.
O Gini Impurity é uma medida utilizada para avaliar a qualidade de uma divisão em um nó da árvore de decisão. Ele mede a impureza ou a mistura de classes em um nó. Quanto menor o valor do Gini Impurity, mais pura é a divisão, ou seja, mais homogêneas são as classes resultantes.
Aqui estão algumas regras que poderiam ser aplicadas ao conjunto de dados:
- Regra baseada no atributo “Horas de Sono”:
- Se a pessoa dorme mais de 7 horas, então a qualidade do sono tende a ser “Boa”.
- Se a pessoa dorme menos de 6 horas, então a qualidade do sono tende a ser “Ruim”.
- Essa regra pode ter um peso significativo, pois a quantidade de horas de sono parece ter uma forte influência na qualidade do sono.
- Regra baseada no atributo “Exercício Físico”:
- Se a pessoa pratica exercícios físicos regularmente, então a qualidade do sono tende a ser melhor.
- Se a pessoa não pratica exercícios físicos, então a qualidade do sono tende a ser pior.
- Essa regra pode ter um peso moderado, pois a prática de exercícios físicos parece ter um impacto positivo na qualidade do sono, mas pode não ser tão determinante quanto as horas de sono.
- Regra baseada no atributo “Estresse”:
- Se a pessoa tem um nível de estresse baixo, então a qualidade do sono tende a ser melhor.
- Se a pessoa tem um nível de estresse alto, então a qualidade do sono tende a ser pior.
- Essa regra pode ter um peso moderado a alto, pois o nível de estresse parece ter uma influência significativa na qualidade do sono.
Agora, vamos considerar o Gini Impurity para avaliar a qualidade dessas regras:
- Regra baseada no atributo “Horas de Sono”:
- Se dividirmos o conjunto de dados com base nas horas de sono (por exemplo, <= 7 horas e > 7 horas), podemos obter uma divisão relativamente pura.
- As pessoas que dormem mais de 7 horas tendem a ter uma qualidade do sono “Boa”, enquanto as que dormem menos tendem a ter uma qualidade do sono “Ruim” ou “Regular”.
- Essa divisão pode resultar em um Gini Impurity relativamente baixo, indicando uma boa separação das classes.
- Regra baseada no atributo “Exercício Físico”:
- Se dividirmos o conjunto de dados com base na prática de exercícios físicos (Sim ou Não), podemos obter uma divisão menos pura em comparação com as horas de sono.
- Embora a prática de exercícios físicos possa influenciar positivamente a qualidade do sono, ainda pode haver uma mistura de classes em cada ramo da divisão.
- O Gini Impurity para essa regra pode ser um pouco maior em comparação com a regra baseada nas horas de sono.
- Regra baseada no atributo “Estresse”:
- Se dividirmos o conjunto de dados com base no nível de estresse (Baixo, Moderado, Alto), podemos obter uma divisão relativamente pura.
- As pessoas com baixo estresse tendem a ter uma qualidade do sono melhor, enquanto as com alto estresse tendem a ter uma qualidade do sono pior.
- O Gini Impurity para essa regra pode ser relativamente baixo, indicando uma boa separação das classes.
É importante ressaltar que essas são apenas análises iniciais baseadas no conjunto de dados fictícios fornecido. Ao construir uma árvore de decisão, o algoritmo avaliará todas as combinações possíveis de atributos e valores de divisão para encontrar as melhores regras que minimizem o Gini Impurity e maximizem a pureza das divisões.
O peso de cada regra pode variar dependendo do conjunto de dados específico e da importância relativa de cada atributo na determinação da qualidade do sono. O algoritmo de árvore de decisão ajustará automaticamente os pesos e selecionará as melhores regras com base nos dados de treinamento.
O processo de construção da árvore envolve a seleção recursiva do melhor atributo para dividir os dados em subconjuntos menores, com base em uma medida de impureza, como o índice Gini ou a entropia. O objetivo é criar uma árvore que minimize a impureza e maximize a separação das classes.
Aqui está um exemplo de código usando o Scikit-Learn para treinar uma Decision Tree com base nos dados fictícios de qualidade do sono:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 |
import numpy as np from sklearn.tree import DecisionTreeClassifier from sklearn.tree import plot_tree import matplotlib.pyplot as plt # Dados de exemplo data = [ ['A', 8, 'Sim', 'Baixo', 'Boa'], ['B', 6, 'Não', 'Alto', 'Ruim'], ['C', 7, 'Sim', 'Moderado', 'Regular'], ['D', 5, 'Não', 'Alto', 'Ruim'], ['E', 9, 'Sim', 'Baixo', 'Boa'], ['F', 6, 'Sim', 'Moderado', 'Regular'], ['G', 7, 'Não', 'Baixo', 'Regular'], ['H', 8, 'Sim', 'Baixo', 'Boa'], ['I', 5, 'Não', 'Alto', 'Ruim'], ['J', 7, 'Sim', 'Moderado', 'Regular'] ] # Convertendo os dados para um array numpy data_array = np.array(data) # Separando os atributos (X) e a classe (y) X = data_array[:, 1:-1] y = data_array[:, -1] # Convertendo os valores categóricos para numéricos X_encoded = [] for row in X: hours = int(row[0]) exercise = 1 if row[1] == 'Sim' else 0 stress = {'Baixo': 0, 'Moderado': 1, 'Alto': 2}[row[2]] X_encoded.append([hours, exercise, stress]) # Criando e treinando a Decision Tree clf = DecisionTreeClassifier() clf.fit(X_encoded, y) # Plotando a árvore de decisão plt.figure(figsize=(12, 8)) plot_tree(clf, filled=True, feature_names=['Horas de Sono', 'Exercício Físico', 'Estresse'], class_names=['Boa', 'Regular', 'Ruim']) plt.show() # Fazendo previsões com novos dados new_data = [[7, 'Sim', 'Baixo'], [6, 'Não', 'Alto'], [8, 'Sim', 'Moderado']] new_data_encoded = [] for row in new_data: hours = int(row[0]) exercise = 1 if row[1] == 'Sim' else 0 stress = {'Baixo': 0, 'Moderado': 1, 'Alto': 2}[row[2]] new_data_encoded.append([hours, exercise, stress]) predictions = clf.predict(new_data_encoded) print("Previsões:", predictions) |
Neste código, estamos utilizando o algoritmo de Árvore de Decisão (Decision Tree) para criar um modelo de classificação baseado em um conjunto de dados de exemplo. O objetivo é entender como o algoritmo funciona e como ele pode ser aplicado para fazer previsões.
Vamos analisar o código em detalhes, com foco no entendimento do algoritmo de Árvore de Decisão:
- Importação das bibliotecas:
numpyé importado para manipulação de arrays.sklearn.treeé importado para utilizar a implementação da Árvore de Decisão.matplotlib.pyploté importado para visualização da árvore de decisão.
- Dados de exemplo:
- Definimos um conjunto de dados de exemplo chamado
data, que consiste em uma lista de listas. - Cada lista interna representa uma amostra de dados, contendo atributos e a classe correspondente.
- Os atributos incluem informações como horas de sono, exercício físico e nível de estresse.
- A classe representa a qualidade do sono, que pode ser “Boa”, “Regular” ou “Ruim”.
- Definimos um conjunto de dados de exemplo chamado
- Separação dos atributos (X) e da classe (y):
- Convertemos a lista
dataem um array NumPy usandonp.array(data). - Separamos os atributos (X) e a classe (y) usando indexação de arrays.
Xcontém todas as linhas e as colunas de índice 1 até a penúltima coluna, representando os atributos.ycontém todas as linhas e a última coluna, representando a classe.
- Convertemos a lista
- Conversão dos valores categóricos para numéricos:
- Como a Árvore de Decisão trabalha com valores numéricos, convertemos os valores categóricos dos atributos para valores numéricos.
- Criamos uma nova lista
X_encodedpara armazenar os valores numéricos. - Percorremos cada linha de
Xe convertemos os valores categóricos para numéricos usando um dicionário de mapeamento.
- Criação e treinamento da Árvore de Decisão:
- Criamos uma instância da classe
DecisionTreeClassifierdo scikit-learn. - Treinamos a árvore de decisão usando o método
fit(), passando os atributos codificados (X_encoded) e as classes correspondentes (y). - Durante o treinamento, o algoritmo de Árvore de Decisão constrói uma árvore binária recursivamente, dividindo os dados com base nos atributos que melhor separam as classes.
- O algoritmo escolhe o melhor atributo para dividir os dados em cada nó da árvore, com base em medidas como o Índice de Gini ou a Entropia.
- Criamos uma instância da classe
- Plotagem da árvore de decisão:
- Utilizamos a função
plot_tree()do scikit-learn para visualizar a árvore de decisão treinada. - Definimos o tamanho da figura usando
figsizee passamos a árvore treinada (clf) como argumento. - Especificamos os nomes dos atributos e das classes para melhorar a interpretabilidade da árvore plotada.
- Utilizamos a função
- Fazendo previsões com novos dados:
- Criamos um novo conjunto de dados chamado
new_data, representando novas amostras para as quais desejamos fazer previsões. - Convertemos os valores categóricos dos novos dados para numéricos, seguindo o mesmo processo usado anteriormente.
- Utilizamos o método
predict()da árvore treinada para fazer previsões com base nos novos dados codificados. - As previsões são armazenadas na variável
predictionse impressas no console.
- Criamos um novo conjunto de dados chamado
|
1 |
Imagem da Arvore |
Vamos analisar alguns dos blocos correspondentes a um nó da árvore de decisão produzida pelo algoritmo.
O primeiro bloco:
Horas de Sono <= 7.5: Isso é o critério de divisão neste nó. As amostras que têm um valor de “Horas de Sono” menor ou igual a 7.5 seguem para o nó filho à esquerda, as outras seguem para o nó filho à direita.gini = 0.66: O índice de Gini mede a impureza deste nó. Um valor de 0 significaria que todas as amostras neste nó pertencem a uma única classe. Um valor de 0.66 sugere que este nó contém uma mistura de várias classes.samples = 10: Há 10 amostras neste nó.value = [3, 4, 3]: Isso descreve a distribuição das classes neste nó. Em um problema de classificação triclassificado como este (com as classes ‘Boa', ‘Regular' e ‘Ruim'), indica que há 3 amostras da classe ‘Boa', 4 amostras da classe ‘Regular' e 3 amostras da classe ‘Ruim'.class = Regular: Isso é a classe majoritária neste nó. Se uma amostra caísse neste nó e não houvesse mais divisões a serem feitas, a classe ‘Regular' seria a previsão para essa amostra.
O segundo bloco é uma continuação da árvore de decisão. Ele representa um nó filho do primeiro nó (aquele para o qual Horas de Sono <= 7.5 é verdadeiro).
O terceiro bloco representa um nó folha, um nó sem nós filhos. Isso é evidenciado pelo fato de que a impureza de Gini neste nó é 0, o que significa que todas as amostras neste nó pertencem a uma única classe, ou seja, todas são ‘Regulares'.
Em resumo, essa árvore de decisão está usando as variáveis Horas de Sono e Estresse para classificar amostras em três classes (‘Boa', ‘Regular' e ‘Ruim'). As previsões são feitas seguindo a árvore de decisão, fazendo as perguntas em cada nó e, por fim, retornando a classe majoritária do último nó alcançado.
O algoritmo de Árvore de Decisão é um método de aprendizado supervisionado que constrói uma árvore binária para tomar decisões com base nos atributos dos dados. Ele seleciona recursivamente o melhor atributo para dividir os dados em cada nó, buscando maximizar a separação das classes. A árvore resultante pode ser usada para fazer previsões em novos dados, seguindo os caminhos da árvore com base nos valores dos atributos.
A Árvore de Decisão é um algoritmo simples e interpretável, capaz de lidar com dados categóricos e numéricos. No entanto, pode ser propenso a overfitting se a árvore se tornar muito profunda. Para mitigar esse problema, técnicas como a poda da árvore podem ser aplicadas.
Em resumo, este código demonstra o uso do algoritmo de Árvore de Decisão para criar um modelo de classificação, treiná-lo com dados de exemplo e fazer previsões em novos dados. A visualização da árvore treinada nos permite entender como as decisões são tomadas com base nos atributos dos dados.
Lembre-se de que este é apenas um exemplo ilustrativo com dados fictícios. Em um cenário real, você precisaria coletar dados reais, realizar o pré-processamento necessário e ajustar os parâmetros da Decision Tree de acordo com o seu problema específico.
Random Forest (Floresta Randômica)
A Random Forest é um algoritmo que combina várias Decision Trees para fazer previsões mais robustas e precisas. Cada árvore na floresta é treinada em um subconjunto aleatório dos dados de treinamento e usa um subconjunto aleatório dos atributos para tomar decisões.
A ideia por trás da Random Forest é que, ao combinar as previsões de várias árvores treinadas de forma independente, é possível reduzir a variância e melhorar a generalização do modelo. Durante a previsão, cada árvore na floresta faz sua própria previsão, e a classe final é determinada por votação majoritária.
Vamos aplicar o algoritmo Random Forest no mesmo conjunto de dados.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 |
import numpy as np from sklearn.ensemble import RandomForestClassifier from sklearn.tree import plot_tree import matplotlib.pyplot as plt # Dados de exemplo data = [ ['A', 8, 'Sim', 'Baixo', 'Boa'], ['B', 6, 'Não', 'Alto', 'Ruim'], ['C', 7, 'Sim', 'Moderado', 'Regular'], ['D', 5, 'Não', 'Alto', 'Ruim'], ['E', 9, 'Sim', 'Baixo', 'Boa'], ['F', 6, 'Sim', 'Moderado', 'Regular'], ['G', 7, 'Não', 'Baixo', 'Regular'], ['H', 8, 'Sim', 'Baixo', 'Boa'], ['I', 5, 'Não', 'Alto', 'Ruim'], ['J', 7, 'Sim', 'Moderado', 'Regular'] ] # Convertendo os dados para um array numpy data_array = np.array(data) # Separando os atributos (X) e a classe (y) X = data_array[:, 1:-1] y = data_array[:, -1] # Convertendo os valores categóricos para numéricos X_encoded = [] for row in X: hours = int(row[0]) exercise = 1 if row[1] == 'Sim' else 0 stress = {'Baixo': 0, 'Moderado': 1, 'Alto': 2}[row[2]] X_encoded.append([hours, exercise, stress]) # Criando e treinando o Random Forest clf = RandomForestClassifier(n_estimators=100) # Usando 100 árvores clf.fit(X_encoded, y) # Escolhendo uma árvore específica para visualização, por exemplo, a primeira árvore estimator = clf.estimators_[0] # Plotando a árvore de decisão escolhida plt.figure(figsize=(20, 10)) plot_tree(estimator, filled=True, feature_names=['Horas de Sono', 'Exercício Físico', 'Estresse'], class_names=['Boa', 'Regular', 'Ruim']) plt.show() # Fazendo previsões com novos dados new_data = [[7, 'Sim', 'Baixo'], [6, 'Não', 'Alto'], [8, 'Sim', 'Moderado']] new_data_encoded = [] for row in new_data: hours = int(row[0]) exercise = 1 if row[1] == 'Sim' else 0 stress = {'Baixo': 0, 'Moderado': 1, 'Alto': 2}[row[2]] new_data_encoded.append([hours, exercise, stress]) predictions = clf.predict(new_data_encoded) print("Previsões:", predictions) |
|
1 |
IMAGEM |
Podemos notar na imagem, que os valores e a divisão quando aplicamos o Random Forest são diferentes. Isso porque a Floresta Aleatória é um conjunto de muitas árvores de decisão, cada uma construída com um subconjunto aleatório dos dados e das características. Isso significa que cada árvore na Floresta Aleatória pode ter uma estrutura diferente e fazer previsões diferentes.
Vamos olhar os nós da Floresta Aleatória que você mencionou:
- O primeiro nó, como na Árvore de Decisão, divide as amostras com base na característica “Estresse”, mas os valores de impureza de Gini, número de amostras e distribuição de classes são diferentes por causa das diferenças nos subconjuntos de dados usados para treinar cada árvore.
- O sub-nó divide as amostras com base na característica “Horas de Sono”, ao contrário da Árvore de Decisão que usava a característica “Estresse” novamente. Esta é uma característica importante da Floresta Aleatória: ao usar subconjuntos aleatórios das características para cada árvore, ela pode encontrar divisões importantes que a Árvore de Decisão pode ter perdido.
- O último nó é um nó folha, representando uma previsão final. Mais uma vez, a distribuição das classes é diferente da Árvore de Decisão, refletindo as diferenças nos dados usados para treinar cada árvore.
Em resumo, a Floresta Aleatória produz uma série de árvores de decisão com estruturas potencialmente diferentes, o que pode levar a diferentes previsões para os mesmos dados. Esta é uma das razões pelas quais a Floresta Aleatória é muitas vezes mais poderosa do que uma única Árvore de Decisão, já que ela pode capturar uma gama mais ampla de padrões nos dados.
Decision Tree e Random Forest com Scikit-Learn e Dataset load_iris()
Agora que entendemos os conceitos básicos da Decision Tree e da Random Forest, vamos aplicá-los a um conjunto de dados real usando o Scikit-Learn. Usaremos o famoso conjunto de dados Iris, que contém medidas de diferentes espécies de flores.
Primeiro, vamos carregar o conjunto de dados e dividi-lo em conjuntos de treinamento e teste:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 |
from sklearn.datasets import load_iris from sklearn.model_selection import train_test_split from sklearn.tree import DecisionTreeClassifier from sklearn.ensemble import RandomForestClassifier from sklearn.metrics import accuracy_score from sklearn.tree import plot_tree import matplotlib.pyplot as plt # Carregando o conjunto de dados Iris iris = load_iris() X = iris.data y = iris.target # Dividindo os dados em conjuntos de treinamento e teste X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42) # Criando e treinando a Decision Tree dt_clf = DecisionTreeClassifier() dt_clf.fit(X_train, y_train) # Criando e treinando a Random Forest rf_clf = RandomForestClassifier(n_estimators=100) rf_clf.fit(X_train, y_train) # Fazendo previsões nos dados de teste dt_predictions = dt_clf.predict(X_test) rf_predictions = rf_clf.predict(X_test) # Calculando a acurácia das previsões dt_accuracy = accuracy_score(y_test, dt_predictions) rf_accuracy = accuracy_score(y_test, rf_predictions) print("Acurácia da Decision Tree:", dt_accuracy) print("Acurácia da Random Forest:", rf_accuracy) # Plotando a árvore de decisão plt.figure(figsize=(12, 8)) plot_tree(dt_clf, filled=True, feature_names=iris.feature_names, class_names=iris.target_names) plt.show() |
Ao executar esse código, você verá uma representação visual da árvore de decisão treinada. Cada nó na árvore representa uma condição de divisão com base em um atributo, e as folhas representam as classes previstas.
Em resumo, a Floresta Aleatória produz uma série de árvores de decisão com estruturas potencialmente diferentes, o que pode levar a diferentes previsões para os mesmos dados. Esta é uma das razões pelas quais a Floresta Aleatória é muitas vezes mais poderosa do que uma única Árvore de Decisão, já que ela pode capturar uma gama mais ampla de padrões nos dados.
A visualização da árvore de decisão pode fornecer insights sobre como o modelo está tomando decisões e quais atributos são mais importantes para a classificação. Você pode ajustar os parâmetros da função plot_tree para personalizar a aparência da visualização, como o tamanho da figura, a escala dos nós e a inclusão de informações adicionais nos nós.
Lembre-se de que, para conjuntos de dados maiores e árvores mais complexas, a visualização pode ficar muito grande e difícil de interpretar. Nesses casos, você pode optar por visualizar apenas uma parte da árvore ou usar outras técnicas de interpretação, como a importância dos atributos.
Entendendo a Máquina de Vetores de Suporte (SVM)
A classificação binária é um dos problemas mais comuns e fundamentais em aprendizado de máquina e ciência de dados. Ela envolve a categorização de dados em duas classes distintas. Por exemplo, pode-se querer classificar e-mails como “spam” ou “não spam”, ou diagnosticar exames médicos como “positivo” ou “negativo” para uma determinada condição. Apesar de sua aparente simplicidade, a classificação binária apresenta desafios únicos, especialmente quando os dados não são facilmente separáveis.
Antes de entrar nos algoritmos de SVM, vamos falar sobre classificação binária.
Classificação Binária
A classificação binária envolve a divisão de dados em duas categorias com base em um conjunto de características. Por exemplo, pode-se querer classificar e-mails como “spam” ou “não spam”, ou diagnosticar exames médicos como “positivo” ou “negativo” para uma doença específica. Os principais desafios nesta tarefa incluem lidar com dados sobrepostos, ruído nos dados e a presença de características irrelevantes.
Problemas e Desafios
Um dos principais problemas na classificação binária é a sobreposição entre as classes, onde alguns pontos de dados de uma classe caem na região da outra classe. Isso é particularmente desafiador em casos onde os dados não são linearmente separáveis, ou seja, não existe uma linha reta que possa separar perfeitamente as duas classes. Mas antes vamos começar com a análise de dados separáveis linearmente.
Considere a imagem a seguir:
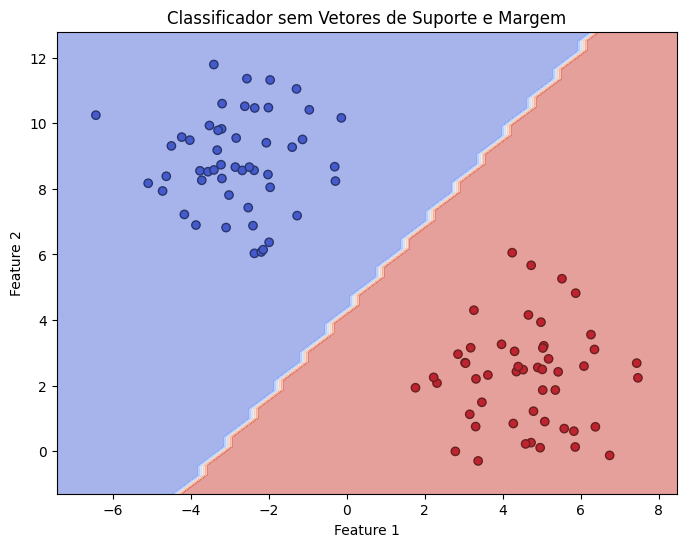
Neste caso, qualquer linha que separe as duas classes seria considerada igualmente boa, independentemente de quão perto os pontos de dados estão da linha. Isso pode levar a uma classificação frágil, onde pequenas variações nos dados de entrada podem resultar em classificações incorretas. A solução para esse problema, pelo menos em dados separáveis linearmente é aplicar o conceito de Margem e Vetores de Suporte.
Uso de Margem e Vetores de Suporte
As Máquinas de Vetores de Suporte (SVM) abordam esses desafios buscando o hiperplano que não apenas separa as duas classes, mas também maximiza a margem entre elas. A margem é definida como a distância entre o hiperplano de decisão e os pontos de dados mais próximos de cada classe, conhecidos como vetores de suporte.
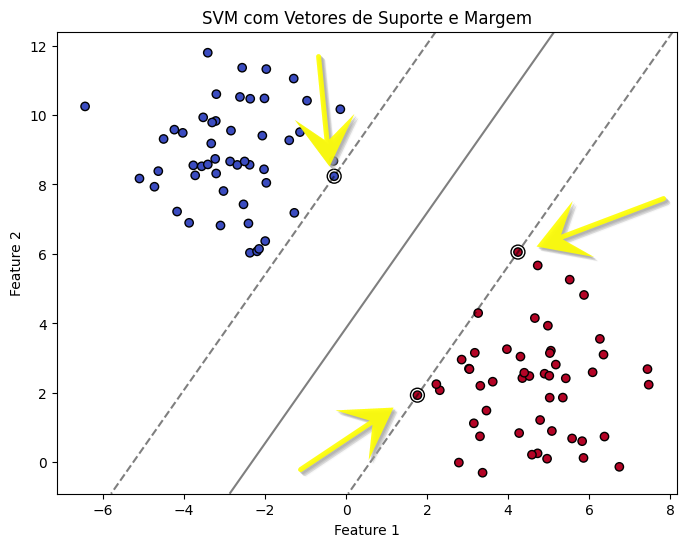
O algoritmo de SVM busca a linha (ou hiperplano, em dimensões maiores) que não apenas separa as duas classes, mas também maximiza a distância (margem) entre a linha e os pontos de dados mais próximos de cada classe (vetores de suporte). Isso resulta em um modelo mais robusto, capaz de generalizar melhor para novos dados.
Isso resolve parte do problema. Mas essa solução não é viável quando os dados não são linearmente separáveis. Quando os dados não são linearmente separáveis, a SVM utiliza o conceito de kernel trick para mapear os dados para um espaço de maior dimensão, onde uma separação linear é possível. O kernel trick é uma técnica poderosa no campo do aprendizado de máquina, especialmente útil em algoritmos que dependem do cálculo do produto interno entre vetores de características, como é o caso das SVMs.
O que é o Kernel Trick?
O kernel trick permite que algoritmos que originalmente operam em espaços de características lineares sejam aplicados em espaços de características transformados, potencialmente de dimensão infinita, sem a necessidade de calcular explicitamente as coordenadas dos dados nesse espaço transformado. Isso é feito substituindo o produto interno padrão por uma função kernel, que computa o produto interno de vetores no espaço transformado de forma indireta.
Um exemplo clássico é o uso do kernel RBF (Radial Basis Function) para dados em forma de círculos concêntricos.
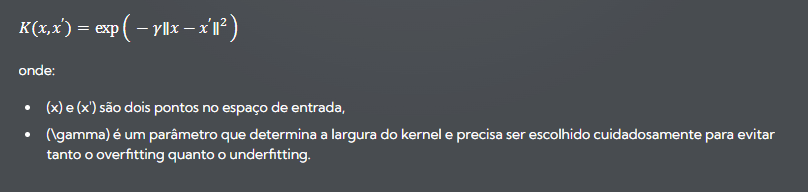
Kernel RBF (Radial Basis Function)
O kernel RBF, também conhecido como kernel gaussiano, é uma função kernel popular que mede a similaridade entre dois pontos de dados. A função RBF é definida como:
Por que o Kernel RBF é Poderoso?
- Não Linearidade: O kernel RBF pode mapear os dados de entrada para um espaço de características de alta dimensão (até infinita), onde os dados que não são linearmente separáveis no espaço original podem se tornar separáveis.
- Flexibilidade: A função RBF é capaz de capturar relações complexas entre os dados devido à sua natureza não linear e ao parâmetro (\gamma), que controla a influência de cada ponto de dados.
- Aplicação do Kernel Trick: Ao usar o kernel RBF, a SVM não precisa transformar explicitamente os dados para o espaço de alta dimensão. Em vez disso, o cálculo do produto interno é substituído pela função kernel RBF, o que torna o processo computacionalmente viável, mesmo para grandes conjuntos de dados.
Portanto, o kernel RBF é um exemplo prático do kernel trick, permitindo que as SVMs lidem eficientemente com problemas de classificação e regressão que envolvem relações complexas e não lineares entre os dados. Ao aplicar o kernel RBF, é possível transformar o problema original em uma forma que pode ser facilmente separada por um hiperplano no espaço de características transformado, sem a necessidade de realizar essa transformação de forma explícita.
Aplicação prática de Kernel Trick para Dados não separáveis linearmente
Considere o seguinte código e a imagem gerada pelo código no google colab:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
import numpy as np import matplotlib.pyplot as plt from sklearn.datasets import make_circles from sklearn.svm import SVC from sklearn.model_selection import train_test_split # Gerando dados sintéticos X, y = make_circles(n_samples=400, factor=0.3, noise=0.1) # Dividindo os dados em conjuntos de treinamento e teste X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42) # Visualizando os dados plt.figure(figsize=(8, 6)) plt.scatter(X[:, 0], X[:, 1], c=y, cmap='viridis', edgecolors='k') plt.title("Dados Não Separáveis Linearmente") plt.xlabel("Feature 1") plt.ylabel("Feature 2") plt.show() |
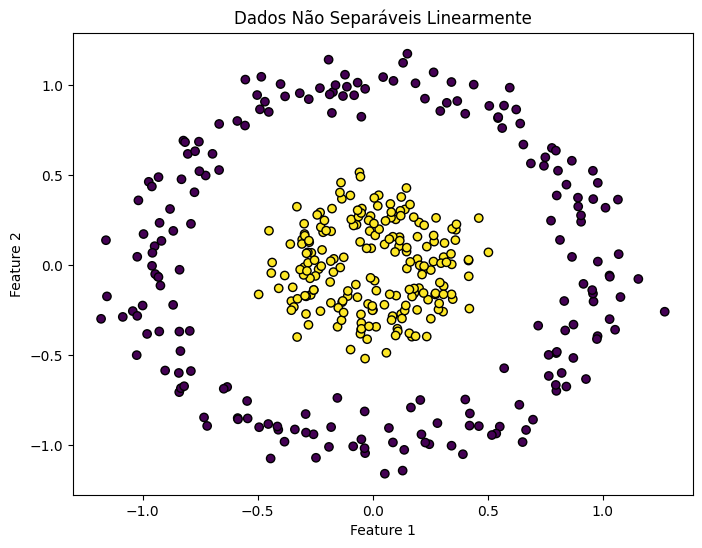
Para lidar com dados como esses, a SVM pode ser equipada com uma função kernel, que permite transformar o espaço de entrada em um espaço de maior dimensão onde os dados se tornam linearmente separáveis. Um dos kernels mais utilizados é o RBF (Radial Basis Function), que pode lidar eficientemente com o problema dos círculos concêntricos.
Observe o código e a imagem a seguir:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
# Treinando o modelo SVM com kernel RBF model = SVC(kernel='rbf', gamma='auto') model.fit(X_train, y_train) # Visualizando a fronteira de decisão plt.figure(figsize=(8, 6)) plt.scatter(X[:, 0], X[:, 1], c=y, cmap='viridis', edgecolors='k') # Criando uma grade para plotar as fronteiras de decisão xx, yy = np.meshgrid(np.linspace(-1.5, 1.5, 500), np.linspace(-1.5, 1.5, 500)) Z = model.predict(np.c_[xx.ravel(), yy.ravel()]) Z = Z.reshape(xx.shape) plt.contourf(xx, yy, Z, alpha=0.75, cmap='viridis') plt.title("Fronteira de Decisão com SVM e Kernel RBF") plt.xlabel("Feature 1") plt.ylabel("Feature 2") plt.show() |
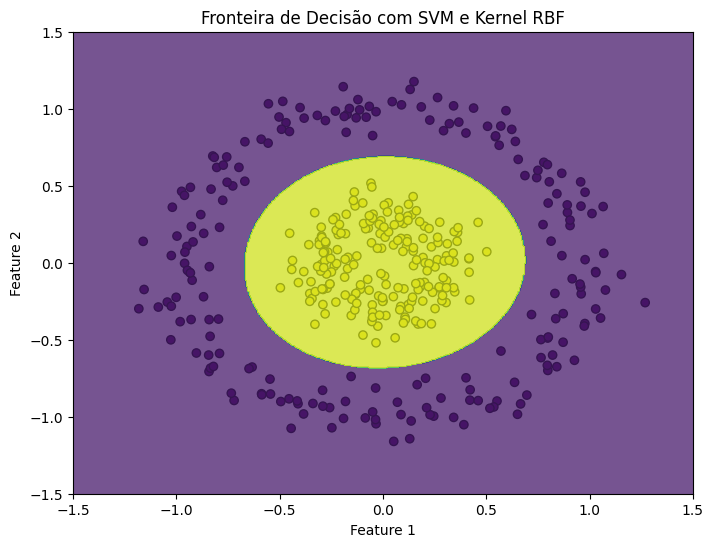
Por Que Não Usar Transformações Polinomiais?
Uma alternativa para lidar com a não linearidade seria aplicar transformações polinomiais aos dados, aumentando o número de características para capturar a complexidade dos dados. No entanto, isso pode levar a um aumento exponencial no número de características, tornando o modelo muito complexo e suscetível a overfitting, além de aumentar significativamente o custo computacional.
Classificação Multiclasse com SVM
A Máquina de Vetores de Suporte (SVM) é um modelo poderoso e versátil de aprendizado de máquina, amplamente utilizado para problemas de classificação binária, onde o objetivo é distinguir entre duas classes. No entanto, muitos problemas do mundo real envolvem a classificação de dados em mais de duas categorias, o que requer uma abordagem de classificação multiclasse. Embora o SVM padrão seja intrinsecamente binário, existem estratégias para adaptá-lo a problemas multiclasse, sendo as mais comuns o One-vs-Rest (OvR, também conhecido como One-vs-All, OvA) e o One-vs-One (OvO).
One-vs-Rest (OvR)
Na estratégia One-vs-Rest, um classificador SVM é treinado para cada classe, para distinguir essa classe de todas as outras. Portanto, se houver (N) classes, (N) classificadores distintos serão treinados. Para um dado classificador, os dados da classe que ele tenta identificar são considerados como a classe positiva, enquanto os dados de todas as outras classes são considerados como a classe negativa.
Quando um novo dado é apresentado para classificação, todos os (N) classificadores são avaliados, e o classificador que apresentar a maior confiança (por exemplo, a maior distância da margem) na sua previsão determina a classe atribuída ao dado. Essa abordagem é relativamente simples e eficaz, especialmente quando a distribuição das classes é desbalanceada, mas pode ser ineficiente se o número de classes for muito grande, pois requer o treinamento de muitos classificadores.
Imagine que você está organizando um campeonato de esportes com vários times. Em vez de fazer todos os times competirem entre si diretamente, como no One-vs-One, você decide realizar uma série de torneios separados. Em cada torneio, um time compete contra todos os outros times juntos. O objetivo é ver o quão bem esse time se sai contra o “resto do mundo”.
Como Funciona o OvR
Para cada time (ou classe, no contexto de classificação), você cria um classificador. Esse classificador tem a tarefa de distinguir o time em questão de todos os outros times. Se você tem (N) times, você terá (N) classificadores diferentes.
- Classificador 1: Distingue o Time 1 de todos os outros times.
- Classificador 2: Distingue o Time 2 de todos os outros times.
- …
- Classificador N: Distingue o Time N de todos os outros times.
Cada classificador é treinado de forma que os dados do time que ele representa são considerados a classe positiva, e os dados de todos os outros times são considerados a classe negativa.
Classificação de Novos Dados
Quando um novo “jogador” (ou ponto de dados) é apresentado, ele é submetido a todos os (N) classificadores. Cada classificador avalia o jogador e fornece uma medida de confiança (por exemplo, a distância da margem no caso de SVMs) sobre a pertinência desse jogador ao time que representa.
O classificador que apresentar a maior confiança na sua previsão determina a qual time o jogador pertence. Essa “confiança” pode ser interpretada como o quão fortemente o classificador acredita que o jogador é membro do seu time.
Vantagens
- Simplicidade: A abordagem OvR é conceitualmente simples e fácil de implementar, pois cada classificador lida com um problema binário.
- Eficiência com Classes Desbalanceadas: OvR pode ser particularmente eficaz em situações onde a distribuição das classes é desbalanceada, pois cada classificador foca em distinguir uma classe das demais.
Desvantagens
- Número de Classificadores: Se o número de classes for muito grande, a necessidade de treinar um classificador para cada classe pode tornar o processo ineficiente.
- Desempenho com Muitas Classes: À medida que o número de classes aumenta, a distinção entre “uma classe” e “todas as outras” pode se tornar menos clara, potencialmente reduzindo a precisão dos classificadores.
A estratégia One-vs-Rest é uma maneira eficiente de transformar classificadores binários em multiclasse, tratando cada problema de classificação como uma série de problemas binários. Embora seja uma abordagem direta e muitas vezes eficaz, a sua eficiência e eficácia podem diminuir à medida que o número de classes aumenta.
One-vs-One (OvO)
Imagine que você está participando de um torneio de jogos com vários times. No caso do OvO, em vez de organizar um grande torneio onde todos competem entre si ao mesmo tempo, você decide fazer séries de partidas, onde cada time enfrenta todos os outros times em jogos individuais.
Como Funciona o OvO
Se você tem (N) times (ou classes, no contexto de classificação), você organiza um jogo (ou treina um classificador) para cada par possível de times. Isso significa que se você tem 3 times, você terá jogos entre Time 1 vs. Time 2, Time 1 vs. Time 3, e Time 2 vs. Time 3.
A Fórmula
A fórmula para calcular o número total de jogos (ou classificadores) que você precisa organizar é:
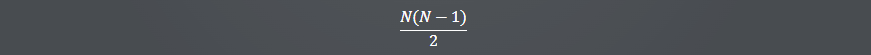
Isso vem do fato de que cada time precisa jogar contra todos os outros times uma vez. Se você listar todos os pares possíveis, verá que a lista cresce rapidamente à medida que você adiciona mais times. A divisão por 2 é porque, por exemplo, o jogo Time 1 vs. Time 2 é o mesmo que Time 2 vs. Time 1, então você não precisa contar ambos.
Exemplo Prático
Se você tem 4 times, o número de jogos necessários seria:
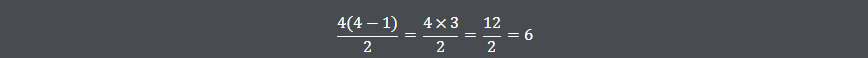
Isso significa 6 jogos no total: Time 1 vs. Time 2, Time 1 vs. Time 3, Time 1 vs. Time 4, Time 2 vs. Time 3, Time 2 vs. Time 4, e Time 3 vs. Time 4.
Classificação de Novos Dados
Quando um novo “jogador” (ou ponto de dados) chega, ele participa de um “jogo” contra cada classificador. Cada classificador vota para decidir a qual time esse jogador pertence. O time que receber mais votos é considerado o vencedor, e o jogador é classificado como membro desse time.
Vantagens
- Precisão: Como cada classificador lida com um problema mais simples (classificação binária entre dois times), essa abordagem pode ser mais precisa, especialmente quando as diferenças entre algumas classes são sutis.
- Complexidade: Cada classificador precisa aprender apenas a distinguir entre duas classes, o que pode ser mais fácil do que aprender a distinção entre várias classes ao mesmo tempo.
Desvantagens
- Computacionalmente Intensivo: O número de classificadores necessários cresce rapidamente à medida que você adiciona mais classes, o que pode tornar essa abordagem computacionalmente cara.
A estratégia OvO é uma maneira eficaz de lidar com problemas de classificação multiclasse, transformando-os em múltiplos problemas de classificação binária. Embora possa ser mais precisa, a necessidade de treinar múltiplos classificadores pode aumentar significativamente o custo computacional, especialmente à medida que o número de classes aumenta.
Classificação Multiclasse com SVM no Scikit-learn na Prática
Quando se trata de aplicar Máquinas de Vetores de Suporte (SVM) para classificação multiclasse usando a biblioteca scikit-learn, as estratégias One-vs-Rest (OvR) e One-vs-One (OvO) são facilmente implementáveis. O scikit-learn automatiza a seleção e aplicação dessas estratégias, permitindo que os usuários se concentrem mais na análise dos dados do que na complexidade da implementação do algoritmo.
Gerando um Conjunto de Dados Sintético
Vamos começar gerando um conjunto de dados sintético bidimensional com três classes:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
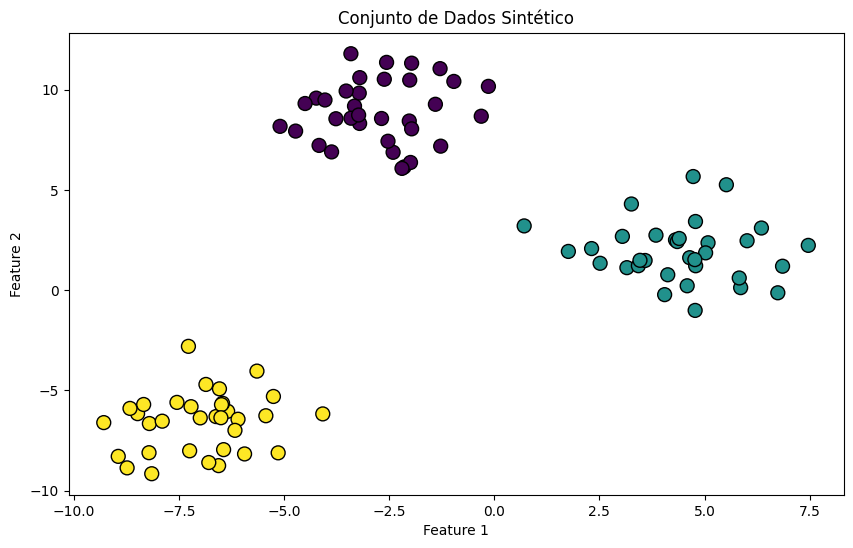
from sklearn.datasets import make_blobs import matplotlib.pyplot as plt import numpy as np # Gerando dados sintéticos X, y = make_blobs(n_samples=100, centers=3, random_state=42, cluster_std=1.5) # Visualizando os dados plt.figure(figsize=(10, 6)) plt.scatter(X[:, 0], X[:, 1], c=y, cmap='viridis', edgecolor='k', s=100) plt.title("Conjunto de Dados Sintético") plt.xlabel("Feature 1") plt.ylabel("Feature 2") plt.show() |
Treinando Modelos SVM com OvR e OvO
Agora, vamos treinar dois modelos SVM, um usando OvR e outro usando OvO, e visualizar as fronteiras de decisão:
|
1 2 3 4 5 6 7 8 9 10 11 |
from sklearn.svm import SVC from sklearn.multiclass import OneVsRestClassifier, OneVsOneClassifier from sklearn.preprocessing import StandardScaler # Normalizando os dados scaler = StandardScaler() X_scaled = scaler.fit_transform(X) # Treinando os modelos model_ovr = OneVsRestClassifier(SVC(kernel='linear', probability=True)).fit(X_scaled, y) model_ovo = OneVsOneClassifier(SVC(kernel='linear', probability=True)).fit(X_scaled, y) |
Visualizando as Fronteiras de Decisão
Para visualizar as fronteiras de decisão, podemos usar uma função auxiliar:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 |
def plot_decision_boundaries(X, y, model, title): # Definindo valores mínimos e máximos e criando uma grade x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1 y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1 xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.1), np.arange(y_min, y_max, 0.1)) # Previsão de cada ponto na grade Z = model.predict(np.c_[xx.ravel(), yy.ravel()]) Z = Z.reshape(xx.shape) # Plotando o resultado plt.contourf(xx, yy, Z, alpha=0.4, cmap='viridis') plt.scatter(X[:, 0], X[:, 1], c=y, cmap='viridis', edgecolor='k', s=100) plt.title(title) plt.xlabel("Feature 1") plt.ylabel("Feature 2") plt.show() # Visualizando as fronteiras de decisão plot_decision_boundaries(X_scaled, y, model_ovr, "Fronteiras de Decisão OvR") plot_decision_boundaries(X_scaled, y, model_ovo, "Fronteiras de Decisão OvO") |
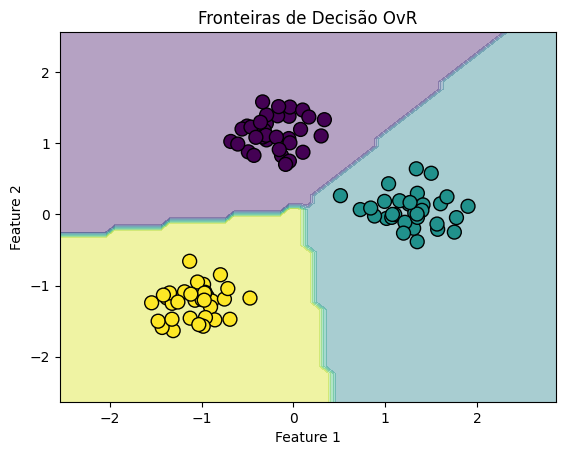
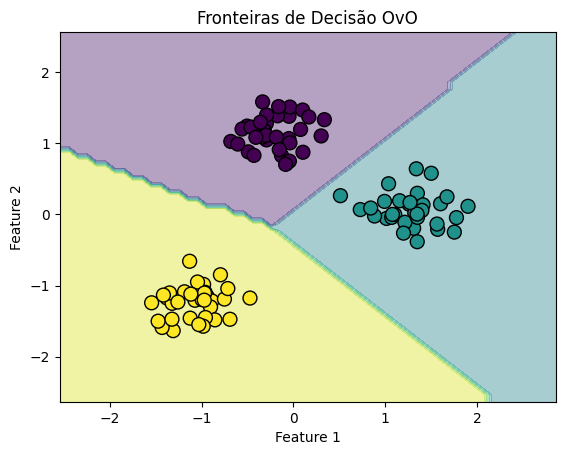
Esses gráficos mostram as fronteiras de decisão geradas por cada estratégia de classificação multiclasse. Embora a diferença possa não ser drasticamente evidente em todos os conjuntos de dados, especialmente em conjuntos de dados simples e bem separados, a escolha entre OvR e OvO pode afetar o desempenho em conjuntos de dados mais complexos e com sobreposição de classes. A visualização ajuda a entender como cada modelo aborda o problema de classificar múltiplas classes, dividindo o espaço de características de maneiras distintas.
Se você quer uma explicação conceitual mais suave dos métodos de classificação OvR e OvO, eu tenho um artigo aqui.
Através dos algoritmos Decision Tree, Random Forest e Support Vector Machine (SVM), exploramos diferentes facetas da classificação, cada uma com suas características únicas, vantagens e desafios.
Decision Tree (Árvore de Decisão)
As árvores de decisão servem como um ponto de partida intuitivo para a classificação, oferecendo modelos facilmente interpretáveis que dividem os dados com base em perguntas sequenciais. Embora sejam simples de entender e implementar, as árvores de decisão podem ser propensas a overfitting, especialmente em cenários com muitas características ou classes.
Random Forest
O Random Forest, um método de ensemble que utiliza múltiplas árvores de decisão para melhorar a precisão e controlar o overfitting, demonstra como a combinação de vários modelos simples pode resultar em um desempenho significativamente melhorado. Esta técnica é particularmente eficaz em lidar com a complexidade inerente aos dados multiclasse e apresenta uma robustez maior contra overfitting, graças à sua natureza agregada.
Support Vector Machine (SVM)
O SVM é um algoritmo poderoso para classificação binária, conhecido por sua capacidade de encontrar a margem ótima entre as classes. A extensão desse algoritmo para problemas multiclasse, através das estratégias One-vs-One e One-vs-Rest, ilustra a flexibilidade dos algoritmos de Machine Learning em adaptar-se a diferentes estruturas de dados e requisitos de classificação.
Classificação Binária vs. Multi-Class Classification
A transição da classificação binária para a multiclasse é um passo significativo que aumenta a complexidade dos problemas de Machine Learning. As estratégias One-vs-One e One-vs-Rest são fundamentais para essa adaptação, permitindo que algoritmos originalmente binários sejam aplicados em cenários com múltiplas classes. Essas estratégias, cada uma com suas peculiaridades, oferecem soluções para expandir a aplicabilidade dos modelos de Machine Learning.
Conclusão Geral
A capacidade de classificar dados com precisão em categorias predefinidas é essencial para muitas aplicações práticas de Machine Learning, desde o reconhecimento de imagens até a filtragem de spam e além. A escolha do algoritmo e da estratégia de classificação depende intrinsecamente da natureza dos dados, do problema em questão e dos requisitos específicos de desempenho e interpretabilidade.
Através da exploração de algoritmos como Decision Tree, Random Forest e SVM, juntamente com a compreensão das abordagens para classificação binária e multiclasse, ganhamos insights valiosos sobre como construir, avaliar e otimizar modelos de classificação. O Python e o Scikit-Learn emergem como ferramentas poderosas nesse contexto, oferecendo uma ampla gama de funcionalidades que facilitam a implementação desses algoritmos complexos de maneira acessível e eficiente.
Em resumo, a classificação em Machine Learning é um campo dinâmico e multifacetado, onde a escolha cuidadosa de algoritmos e estratégias pode levar a modelos altamente eficazes e precisos, capazes de desvendar padrões complexos em dados e fornecer insights valiosos para a tomada de decisões informadas.